CBSE Class 10 Maths Answer Key Term 2: CBSE Class 10 students must be waiting for the answer key of Maths paper that was conducted on 5th May, 2022. We have come here with the solutions created by the subject experts. Therefore, students can check now correct answers to all questions given in the CBSE Class 10 Maths (Standard) Term 2 Question Paper 2022. They can also download the question paper in PDF here and check the paper analysis along with the students' feedback as well.
| CBSE Class 10 Maths (Standard) Term 2 Question Paper 2022 (PDF) |
| CBSE Class 10 Maths Term 2 Paper Analysis and Students' Feedback |
Check CBSE Class 10 Maths (Standard) Answer Key below:
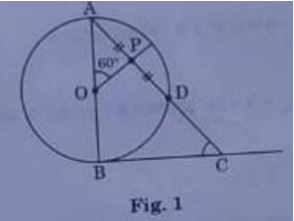
1. In fig. 1, AB is diameter of a circle centered at O. BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find m∠C.
Solution:
Given OP bisect the chord AD.
∴ OP⟂AD
∠P = 900
and ∠B = 900
∠BOP = 1800 - 600 = 1200
Now, in quad. BOPC, applying angle sum property
∠P + ∠B + ∠O + ∠C = 3600
900 + 900 + 1200+ ∠C = 3600
∠C = 3600 - 300 = 600
OR
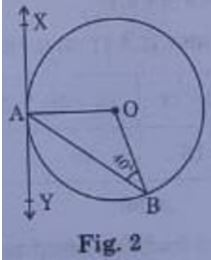
(b) In Fig. 2, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find m∠BAY and m∠AOB.
Solution:
Given ∠ABO = 400
∠XAO = 900
OA = OB (Radii of same circle)
⇒∠OAB = ∠OBA
∴ ∠OAB = 400
Now, applying linear pair of angles property
∠BAY + ∠OAB + ∠XAO = 1800
∠BAY + 400 + 900 = 1800
∠BAY + 1300 = 1800
∠BAY = 500
Now, in ΔAOB,
∠AOB + ∠OAB + ∠OBA = 1800
∠AOB + 400 +400 = 1800
∠AOB + 800 = 1800
∠AOB = 1000
2. If the mode of the following frequency distribution is 55, then find the value of x.
| Class | 0-15 | 15-30 | 30-45 | 45-60 | 60-75 | 75-90 |
| Frequency | 10 | 7 | x | 15 | 10 | 12 |
Solution:
Given that mode of frequency distribution is 55.
Here given mode =55
So, mode class is 45−60
lower limit (t) =45
class height (h) =15
then, f0 =15
f1 =x
f2=10
10(30−x−10)=(15−x)15
10(20−x)=225−15x
200−10x=225−15k
15x−10x=225−200
5x=25
x=5
3. (a) In an AP if some of third and seventh terms is zero, find its 5th term.
Solution:
Let a and d be the first term and common difference of AP
nth term of AP, an=a+(n−1)d
∴a3=a+(3−1)d=a+2d
a7=a+(7−1)d=a+6d
Given a3+a7=0
∴(a+2d)+(a+6d)=0
⇒2a+8d=0
⇒a+4d=0
Now, 5th term of given AP is,
a5=a+(5−1)d=a + 4d
a5= 0
OR
(b) Determine the AP whose third term is 5 and seventh term is 9.
Solution:
We know that
an=a+(n−1)d
∴a3=a+(3−1)d=a+2d
⇒ a+2d = 5 .....(i)
a7=a+(7−1)d=a+6d
⇒ a+6d = 9 .....(ii)
Subtracting (ii) from (i), we have
4d = 4
d = 1
substituting d=2 in (i),
a + 2(1) = 5
a = 5-2
a=3
Thus, first term of required AP is
a = 3
second term = first term + common difference
a2 = 3+1 =4
Similarly, a3 = 4+1 =5, a4 = 6 and so on
Thus, the required AP is 3, 4, 5, 6, .......
4. Solve the quadratic equation x2 + 2√2x - 6 = 0.
5. Find the sum of first 20 terms of an AP whose nth term is given as an = 5 - 2n.
6. A solid piece of metal in the form of a cuboid of dimensions 11 cm x 7 cm x 7 cm is melted to form ‘n’ number of solid spheres of radii 7⁄2 cm each. Find the value of n.
Our experts are developing answers to the remaining questions. Keep visiting this page to know the correct answers to all questions asked in the CBSE Class 10 Term 2 Paper 2022.
Also Read:
CBSE Class 10 Subject-Wise Practice Papers for Term 2 Exam 2022 (By Experts)
CBSE Class 10 Subject-Wise Long & Short Questions for Term 2 Exam 2022 (By Experts)
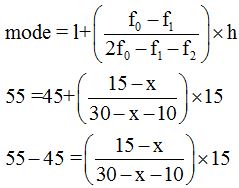
Comments
All Comments (0)
Join the conversation