CBSE Class 9 Maths Sample Paper for the Term 2 Exam 2022 is provided for students to practice important questions and understand the latest paper pattern. This sample paper is curated by experienced teachers to help students prepare important questions for the exam. CBSE Class 9 Maths Sample Paper is prepared according to the latest paper pattern for Term 2. Download the sample paper and its solution in PDF from the links mentioned below in the article.
| CBSE Class 9 Sample Papers with Solutions for Term 2 Exam 2022 (All Subjects) |
Check CBSE Class 9 Maths Sample Paper for Term 2 Exam 2022 below:
Time Allowed: 90 minutes
Max Marks: 40
General Instructions:
1. The question paper consists of 14 questions divided into 3 sections A, B, and C.
2. All questions are compulsory.
3. Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
4. Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
5. Section C comprises of 4 questions of 4 marks each. Internal choice has been provided in one question.
Also, Read
CBSE Class 9 Science Sample Paper for Term 2 Exam 2022
CBSE Class 9 English Sample Paper for Term 2 Exam 2022
Section A
1. The hollow sphere, in which the circus motorcyclist performs his stunts, has a diameter of 7 m. Find the area available to the motorcyclist for riding. (2)
2. Prove that if chords of congruent circles subtend equal angles at their centers, then the chords are equal. (2)
OR
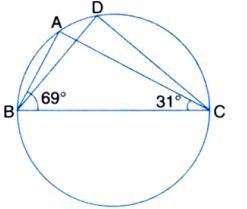
In fig, ∠ABC= 690, ∠ ACB=310. Find ∠BDC.
3.Diagonal AC of a parallelogram ABCD bisects ∠A. Show that it bisects ∠C also. (2)
4.If x2-x-42 = (x+k) (x+6), then find the value of k. (2)
OR
Find the value of x+y+z, if x2+y2+z2=18 and xy+yz +zx=9.
5.ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC=550 and ∠BAC= 450, find ∠BCD. (2)
6.Construct an equilateral triangle, given its side and justify the construction. (2)
Section B
7.Find the possible expressions for length and breadth of the following rectangle in which area is given:
Area: 25a2 -35a + 12. (3)
8.Construct a triangle ABC in which BC= 7 cm, ∠B= 750 and AB + AC=13 cm. (3)
OR
Construct a triangle PQR in which QR=6 cm, ∠Q=600 and PR-PQ =2 cm.
9.Use the factor theorem to determine whether g(x) is a factor of p(x) in each of the following case (3)
P(x)=x3 +3x2+ 3x +1, g(x) = x+2. (3)
10.A hemispherical dome of a building needs to be painted. If the circumference of the base of the dome is 17.6 m, find the cost of painting it, given the cost of painting is Rs. 5 per 100 cm. (3)
Section C
11.Factorise: 2x2 + y2+ 8z2- 2√2xy + 4√2yz - 8xz. (4)
OR
Without actually calculating the cubes, find the value of:
(28)3 + (-15)3 + (-13)3
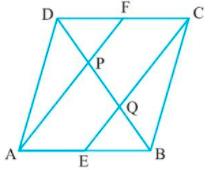
12.In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD. (4)
13.Four friends Rahul, Arun, Ajay, and Vijay went for a picnic at a hill station. They decided to make a conical tent at a park. They were carrying 200 m2 cloth with them. They made the conical tent with a height of 8 m and a diameter of 12 m. The remaining cloth was used for floor.
a) Find the volume of air in the tent?
b) Find the cloth left for the floor after making the tent?
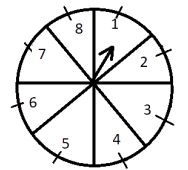
14.One day Rahul visited a park along with his friend. There he saw a game of chance that consists of spinning an arrow that comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 and these equally likely outcomes.
a) Find the probability that the arrow will point at a number greater than or equal to 2.
b) Find the probability that the arrow will point at a number divisible by 3.
Download sample paper and solution (marking scheme) from the following links:
Also Read:

Comments
All Comments (0)
Join the conversation