Class 10 Maths NCERT Solutions Exercise 10.2: Class 10 Maths Exercise 10.2 of Chapter - Circles includes problems relating to more than one tangent to a circle from a common point outside the circle. The basic concepts used in this exercise are as follows:
- The tangent to a circle is perpendicular to the radius through the point of contact.
- The lengths of tangents drawn from an external point to a circle are equal.
Students must solve all the questions given in the exercise to gain a thorough understanding of circle concepts and excel in solving tangent-related problems.
In this article, you will find precise and detailed explanations for all Class 10 Maths Exercise 10.2 questions. The NCERT solutions provided here have been crafted by the subject matter experts. All the solutions are designed to provide students with a comprehensive understanding of tangent concepts and enhance their problem-solving abilities. This will, in turn, help them perform well in their upcoming class 10 board exams.
Highlights of NCERT Solutions for Class 10 Maths Exercise 10.2
| Particulars | Details |
| Subject | Mathematics |
| Chapter Number | 10 |
| Chapter Name | Circles |
| Number of Questions | 13 |
| Number of Short Answer Type Questions | 5 |
| Number of Long Answer Type Questions | 8 |
| Topics covered | Problems involving more than one tangent from the same point outside a circle
|
Check solutions to all questions below:
NCERT Solutions for Class 10 Maths Circles - Exercise 10.2
In Q.1 to 3, choose the correct option and give justification.
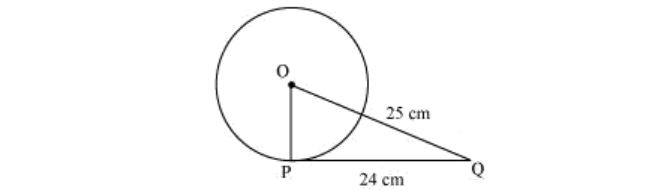
1. From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
Solution:
Let O be the centre of the circle.
Given that,
OQ = 25cm and PQ = 24 cm
OP ⊥ PQ (radius is perpendicular to the tangent at the point of contact)
Applying Pythagoras theorem in ΔOPQ,
OP2 + PQ2 = OQ2
OP2 + 242 = 252
OP2 = 625 − 576
OP2 = 49
OP = 7
Therefore, the radius of the circle is 7 cm.
Hence, alternative (A) is correct
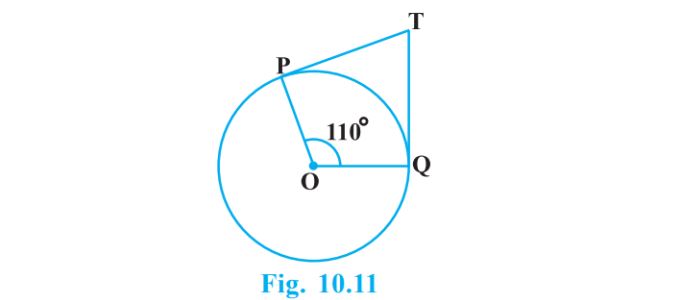
2. In Fig. 10.11, if TP and TQ are the two tangents to a circle with centre O so that∠POQ = 110°, then ∠PTQ is equal to
(A) 60°
(B) 70°
(C) 80°
(D) 90°
Solution:
It is given that TP and TQ are tangents.
Therefore, radius drawn to these tangents will be perpendicular to the tangents.
Thus, OP ⊥ TP and OQ ⊥ TQ
∠OPT = 90o
∠OQT = 90o
In quadrilateral POQT,
Sum of all interior angles = 360o
∠OPT + ∠POQ +∠OQT + ∠PTQ = 360o
⇒ 90o + 110o + 90o +∠PTQ = 360o
⇒ ∠PTQ = 70o
Hence, alternative (B) is correct.
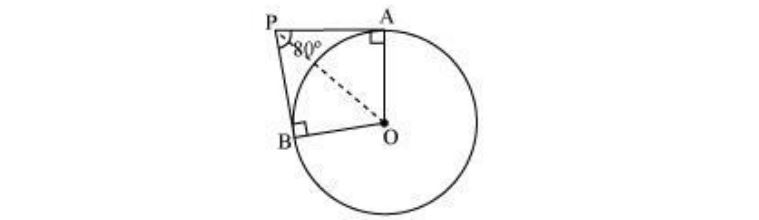
3. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then POA is equal to
(A) 50°
(B) 60°
(C) 70°
(D) 80°
Solution:
It is given that PA and PB are tangents.
Therefore, the radius drawn to these tangents will be perpendicular to the tangents.
Thus, OA ⊥ PA and OB ⊥ PB
∠OBP = 90o
∠OAP = 90o
In AOBP,
Sum of all interior angles = 360o
∠OAP + ∠APB +∠PBO + ∠BOA = 360o
90o + 80o + 90o +∠BOA = 360o
∠BOA = 100o
In ΔOPB and ΔOPA,
AP = BP (Tangents from a point)
OA = OB (Radii of the circle)
OP = OP (Common side)
Therefore, ΔOPB ≅ΔOPA (SSS congruence criterion)
A ↔ B, P ↔ P, O ↔ O
And thus, ∠POB = ∠POA
∠POA = 1/2∠AOB = 100/2 = 50o
Hence, alternative (A) is correct.
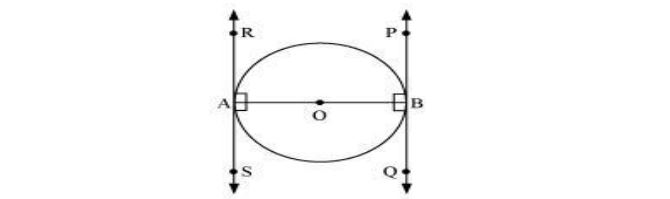
4. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Solutions:
Let AB be the diameter of the circle. Two tangents PQ and RS are drawn at points A and B
respectively.
Thus, OA ⊥ RS and OB ⊥ PQ
∠OAR = 90o
∠OAS = 90o
∠OBP = 90o
∠OBQ = 90o
It can be observed that
∠OAR = ∠OBQ (Alternate interior angles)
∠OAS = ∠OBP (Alternate interior angles)
Since alternate interior angles are equal, lines PQ and RS will be parallel.
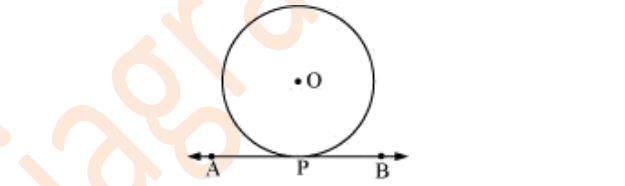
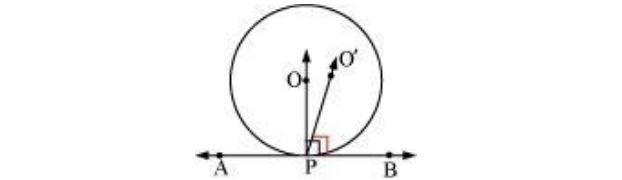
5. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Solution: Let us consider a circle with centre O. Let AB be a tangent which touches the circle at P.
Let us assume that the perpendicular to AB at P does not pass through centre O. Let it pass through
another point O’.
Join OP and O’P
As perpendicular to AB at P passes through O’, therefore,
∠O’PB = 90° ……….. (1)
Line joining the centre and the point of contact to the tangent of the circle are perpendicular to each
other.
∴ ∠OPB = 90° ………. (2)
Comparing equations (1) and (2), we obtain
∠O’PB = ∠OPB ………. (3)
From the figure, it can be observed that,
∠O’PB < ∠OPB ……….. (4)
Therefore, ∠O’PB = ∠OPB is not possible. It is only possible, when the line O’P coincides with OP.
Therefore, the perpendicular to AB through P passes through centre O.
Check and download all the NCERT solutions from the link given below:
Also Check

Comments
All Comments (0)
Join the conversation