Trigonometry is the branch of mathematics that explains the relationship between sides and angles of a triangle.
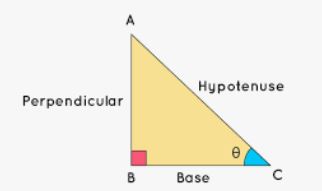
In a right angled triangle the three sides are perpendicular, base and hypotenuse, as shown in the image below.
There are three main trigonometric functions - Sine θ (sin θ), Cosine θ (cos θ) and Tangent θ (tan θ).
Sin θ - Ratio of Perpendicular to Hypotenuse
Cos θ - Ratio of Base to Hypotenuse
Tan θ - Ratio of Perpendicular to Base
Tips and Tricks to Learn Trigonometric Formulas, Table and Signs Easily
There are few easy ways to learn the trigonometric formulas and their signs in each quadrant.
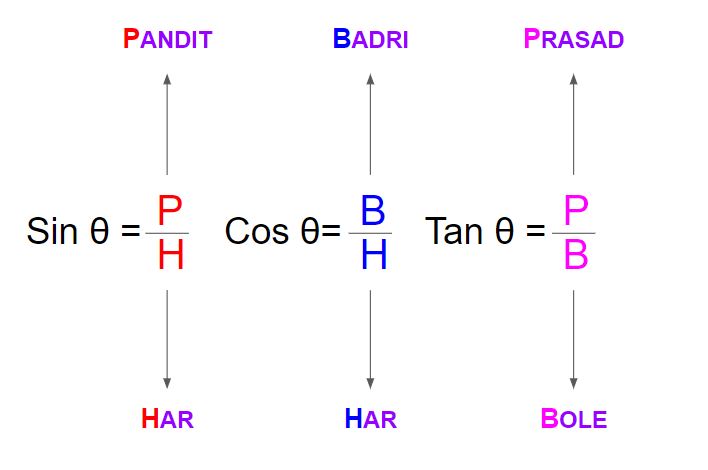
1.Pandit Badri Prasad Har Har Bole
P from Pandit is for Perpendicular and H from Har is for Hypotenuse, B from Badri is for Base and H from Har (in the middle) is for Hypotenuse and P from Prasad is for Perpendicular and B from Bole is for Base (reference image below).
![]()
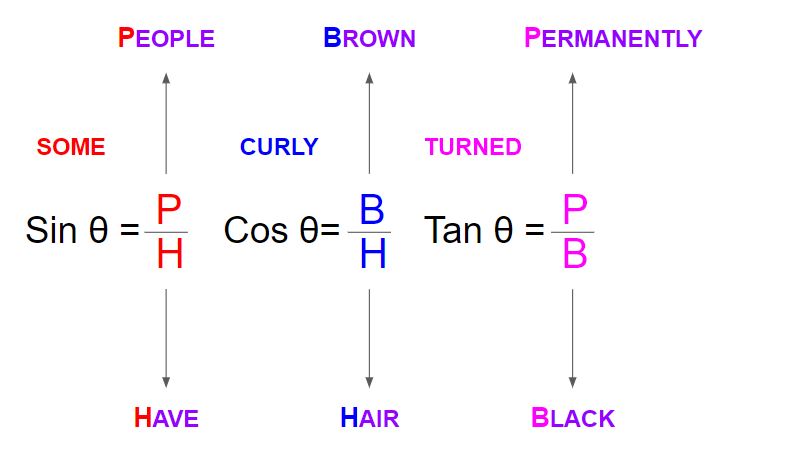
2. Some People Have Curly Brown Hair Turned Permanently Black
S from Some is for Sin, P from People is for Perpendicular and H from Have is for Hypotenuse, C from Curly is for Cos, B from Brown is for Base and H from Hair is for Hypotenuse and T from Turned is for Tan, P from Permanently is for Perpendicular and B from Black is for Base (reference image below).
3. Add Sugar To Coffee (ASTC)
There are four quadrants and ASTC techniques helps you remember if a trigonometric function is positive or negative in each quadrant.
ADD - All (Sin, Cos, Tan) are positive
SUGAR - Sin is positive, Cos and Tan are negative
TO - Tan is positive, Sin and Cos are negative
COFFEE - Cos is positive, Sin and Tan are negative
4. Hand Trick to Learn the Trigonometry Table
Trigonometry Table is a table that helps us to calculate the values of trigonometric ratios for common angles such as 0°, 30°, 45°, 60°, and 90°. But it is difficult to memorise the values. So here it is a simple hand trick to write the value of the trigonometric ratios.
Take your left hand and assign an angle to each finger as shown below.
Sin = √Fingers below / 2
Cos = √Fingers above / 2
For example-
Sin 60° = √Fingers below 60° finger/2 = √3/2
Cos 90° = √Fingers above 90° finger/2 = √0/2 = 0
To calculate the tan ratios, flip the hand and assign the angles as shown below.
Tan = √Fingers above/ √Fingers below
For example-
Tan 30° = √Fingers above 30° finger / √Fingers below 30° finger = √1 / √3 = 1/√3
Important Trigonometry Formulas
| S.no | Property | Mathematical value |
| 1 | sin θ | Perpendicular/Hypotenuse |
| 2 | cos θ | Base/Hypotenuse |
| 3 | tan θ | Perpendicular/Base |
| 4 | cot θ | Base/Perpendicular |
| 5 | cosec θ | Hypotenuse/Perpendicular |
| 6 | sec θ | Hypotenuse/Base |
Reciprocal Trigonometry Formulas
| S.no | Identity | Relation |
| 1 | tan θ | sin θ/cos θ |
| 2 | cot θ | cos θ/sin θ |
| 3 | cosec θ | 1/sin θ |
| 4 | sec θ | 1/cos θ |
Hope this helps you memorise trigonometric basic formulas, their signs in each quadrant and trigonometry table.
Also Read
Tricky Math Riddle: Test Your Wits By Finding The Next Number In The Series In 41 Seconds!
Seating Arrangement Question With Answer - Only Brilliant Minds Can Solve This
All Trigonometry Formulas and Identities: Full Formula List From Basic To Advanced Maths



Comments
All Comments (0)
Join the conversation