CBSE Class 12 Applied Mathematics Sample Question Paper 2022-23: Class 12 Applied Mathematics Sample Paper 2022-23 (code 241) has been released by CBSE. CBSE has also released the marking scheme for the same. It is now available on their website. You can view and download both the documents, in pdf format, at Jagran Josh.
While introducing Applied Mathematics course in 2020, CBSE mentioned that in higher education, mathematics is frequently employed as a complementary subject in the fields of economics, commerce, social sciences, etc. According to observation, students who pursue Commerce or Social Science in college may not be able to use the senior secondary mathematics curriculum designed for science topics. In order to give students useful Mathematics skills that may be applied to areas other than the physical sciences, one more elective course in the mathematics curriculum for senior secondary schools is established with this in mind.
Although the course is relatively new, there’s no reason to worry.
You can download the prescribed syllabus for Applied Mathematics 2022-23 here.
Let us start with the CBSE 12 Applied Mathematics Sample Question Paper.
The sample question paper begins with the general instructions for the students to follow.
The general instructions in the beginning of the CBSE Class 12 Applied Mathematics Sample Question Paper 2022-23 are as follows:
TIME - 3 HOURS
MAX. MARKS - 80
General Instructions:
1. This question paper contains five sections A, B, C, D and E. Each section is compulsory.
2. Section - A carries 20 marks weightage, Section - B carries 10 marks weightage, Section - C carries 18 marks weightage, Section - D carries 20 marks weightage and Section - E carries 3 case-based with total weightage of 12 marks.
SECTION – A
(All questions are compulsory. No internal choice is provided in this section)
1. What is the least value of ‘𝑥’ that satisfies 𝑥≡ 27(mod 4), when 27<𝑥≤36?
a) 27
b) 30
c) 31
d) 35
2. Let 𝑝>0 and 𝑞<0 and 𝑝,𝑞∈𝑍, then choose the correct inequality from the given below options to complete the statement:

a) >
b) ≤
c) ≥
d) <
3. A machine makes car wheels and in a random sample of 26 wheels, the test statistic is found to be 3.07. As per the t-distribution test (of 5% level of significance), what can you say about the quality of wheels produced by the machine? (Use t25(0.05) = 2.06)
a) Superior quality
b) Inferior quality
c) Same quality
d) Cannot say
4. For the purpose of t-test of significance, a random sample of size (𝑛) 34 is drawn from a normal population, then the degree of freedom (𝑣) is -
a) 1/34
b) 33
c) 34
d) 35
5. A person can row a boat along the stream of the river at 10 km/h and against the stream in 6 km/h. What is the speed of the stream flow?
a) 1 km/h
b) 2 km/h
c) 4 km/h
d) 5 km/h
6. Standard deviation of a sample from a population is called a -
a) Standard error
b) Parameter
c) Statistic
d) Central limit
7. Two water supplying trucks – A and B supply water to remote areas. Truck A is carrying 100 litres of water to a village 1.5 km away and truck B is delivering 80 litres of water to another village, 1 km away. Due to bad road conditions, each truck loses 20 ml water while travelling each metre distance. Which truck is able to deliver more water and by how much more?
a) Truck A, 20 litres
b) Truck B, 20 litres
c) Truck A, 10 litres
d) Truck B, 10 litres
8. What is the face value of a sinking fund that yields a dividend of ₹1800 at 10% semi-annually?
a) Rs. 3600
b) Rs. 18000
c) Rs. 24000
d) Rs. 36000
9. In the given figure, the area bounded by the curve 𝑥=𝑓(𝑦), 𝑦 -axis and abscissa 𝑦=𝑎 and 𝑦=𝑏 is equal to -

a) ∫ab𝑓(𝑦)𝑑𝑦
b) ∫ab𝑓 (𝑥)𝑑𝑥
c) ∫ab |𝑓(𝑦)| 𝑑𝑦
d) ∫ab |𝑓(𝑥)| 𝑑𝑥
10. A factory production is delayed for three weeks due to breakdown of a machine and unavailability of spare parts. Under which trend oscillation does this situation fall under?
a) Seasonal
b) Cyclical
c) Secular
d) Irregular
11. A newspaper printing machine costs Rs. 4,80,000 and estimated scrap value of Rs. 25,000 at the end of its useful life of 10 years. What is its annual depreciation as per linear method?
a) Rs. 4,550
b) Rs. 45,500
c) Rs. 50,500
d) Rs. 61,500
12. In the given figure (I), what is the LPP shaded region known as?

a) Feasible region
b) Feasible solution
c) Optimal region
d) Objective region
13. General solution of differential equation: 𝑦𝑙𝑜𝑔𝑦 𝑑𝑥−𝑥 𝑑𝑦=0 is –
a) 𝑦=log|𝐶𝑥|
b) 𝑦=𝑒|𝐶𝑥|
c) 𝑦 =𝑒−𝐶𝑥
d) log𝑦=|𝐶+𝑥|
14. An investment of Rs. 10,000 becomes Rs. 60,000 in 4 years, then the CAGR (compound annual growth rate) is given by -
a) 4√6−1100
b) 4√6+1100
c) [4√6−1]×100
d) [4√6+1]×100
15. In what ratio shall I add water to the liquid detergent costing Rs. 480 per litre to get resulting mixture worth Rs. 300 per litre?
a) 5:3
b) 3:8
c) 3:5
d) 5:8
16. A grain whole-seller visits the granary market. While going around to make a good purchase, he takes a handful of rice from random sacks of rice, in order to inspect the quality of farmers produce. The handful of rice taken from a sack of rice for quality inspection is a:
a) statistic
b) population
c) parameter
d) sample
17. For predicting the straight-line trend in the sales of scooters (in thousands) on the basis of 6 consecutive years data, the company makes use of 4-year moving averages method. If the sales of scooters for respective years are 𝑎,𝑏,𝑐,𝑑,𝑒 and 𝑓 respectively, then which of the following average will not be computed?
a) 𝑎+𝑏+𝑐+𝑑/4
b) 𝑏+𝑐+𝑑+𝑒/4
c) 𝑎+𝑐+𝑑+𝑒/4
d) 𝑐+𝑑+𝑒+𝑓/4
18. In a school, a random sample of 145 students is taken to check whether a student’s average calory intake is 1500 or not. The collected data of average calories intake of sample students is presented in a frequency distribution, which is called a:
a) Statistics
b) Sampling distribution
c) Parameter
d) Population sampling
For questions 19 and 20, two statements are given – one labelled Assertion(A) and the other labelled Reason (R). Select the correct answer to these questions from the codes (i), (ii), (iii) and (iv) as given below:
(i) Both A and R are true and R is the correct explanation of the assertion
(ii) Both A and R are true but R is not the correct explanation of the assertion
(iii) A is true, but R is false
(iv) A is false, but R is true
19. Assertion (A) : Kuhu and Beena are two equally capable badminton players. Probability that Beena will beat Kuhu in 3 games out of 4 is 25%
Reason (R) : The probability of 𝑟 successes in 𝑛 trials, denoted by P(X = 𝑟) is given by
P(X = 𝑟) = nCr 𝑝𝑟𝑞𝑛−𝑟 , 𝑟= 0, 1,...,𝑛 where 𝑝 denotes success and 𝑞 denotes failure in each trial.
a) (i)
b) (ii)
c) (iii)
d) (iv)
20. Assertion (A) : If the nominal rate of interest is 12.5% and the inflation is 2%, then the effective rate of interest is 10.5%
Reason (R) : If the interest is calculated only at the end of an year, then the effective rate of interest is same as the nominal rate of interest.
a) (i)
b) (ii)
c) (iii)
d) (iv)
SECTION – B
(All questions are compulsory. In case of internal choice, attempt any one question only)
21. Rs. 2,50,000 cash is equivalent to a perpetuity of Rs. 7,500 payable at the end of each quarter. What is the rate of interest convertible quarterly?
22.
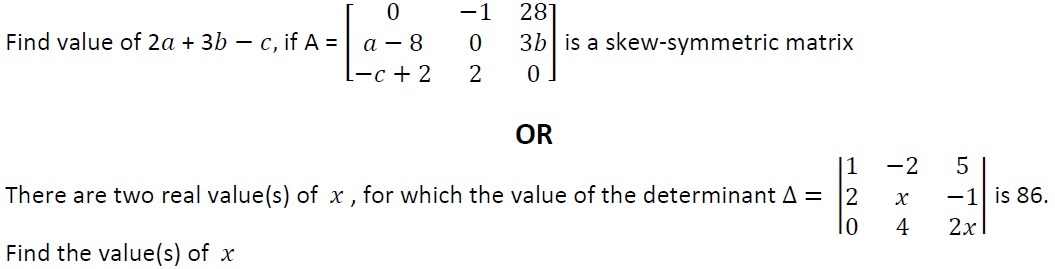
23. A book publisher sells a hard cover edition of a book for Rs. 72 and a paperback edition for Rs. 40. In addition to a fixed weekly cost of Rs. 9,600, the cost of printing hardcover and paperback editions are Rs. 56 and Rs. 28 per book respectively. Each edition requires 5 minutes on the printing machine whereas hardcover binding takes 10 minutes and paperback takes 2 minutes on the binding machine. The printing machine and the binding machine are available for 80 hours each week. Formulate the linear programming problem to maximise the publisher’s profit.
24. A boatman takes half as much time in rowing his boat for a certain distance downstream than upstream. What is the ratio between his speed of rowing the boat in still water and speed of current?
OR
In a 200-metre race, Anuj can beat Param by 5 metre or 3 seconds. How much time did Anuj take to complete the race?
25. Mitul invested Rs. 3,50,000 in a fund. At the end of the year the value of the fund is Rs. 4,37,500. What is the nominal rate of interest, if the market price is same at the end of the year?
SECTION – C
(All questions are compulsory. In case of internal choice, attempt any one question only)
26. Find the interval(s) in which the function 𝑓(𝑥)= 𝑥4/4−2𝑥3+11𝑥2/2−6𝑥, is strictly increasing and strictly decreasing.
27. Two badminton teams A and B are staying in the same hotel. Team A has 2 male and 3 female players accompanied by 1 coach. Team B comprises of 1 male, 2 female players and 2 coaches. The daily diet requirement (calories and protein) for each person is as given below:
|
| Calories | Protein |
| Male player | 2500 | 65 g |
| Female player | 1900 | 50 g |
| Coach | 2000 | 54 g |
Use matrix algebra to calculate the total diet requirement of calories and protein for each team.
28. Evaluate ∫𝑑𝑥/(1+𝑒𝑥)(1+𝑒−𝑥)
OR
Evaluate ∫𝑥 𝑙𝑜𝑔(1+𝑥2) 𝑑𝑥
29. Under the pure market competition scenario, the demand function 𝑝𝑑 and the supply function 𝑝𝑠 for a certain commodity are given as 𝑝𝑑= (8/𝑥+1)−2 and 𝑝𝑠 = 𝑥+3/2 respectively, where 𝑝 is the price and 𝑥 is the quantity of the commodity. Using integrals, find the producer’s surplus.
Or
The demand function 𝑝 for maximising a profit monopolist is given by 𝑝 = 274 −𝑥2 while the marginal cost is 4 + 3𝑥, for 𝑥 units of the commodity. Using integrals, find the consumer surplus.
30. Surjeet purchased a new house, costing Rs. 40,00,000 and made a certain amount of down payment so that he can pay the balance by taking a home loan from XYZ Bank. If his equated monthly installment is Rs. 30,000, at 9% interest compounded monthly (reducing balance method) and payable for 25 years, then what is the initial down payment made by him? [Use (1.0075)−300= 0.1062]
31. 10 years ago, Mr Mehra set up a sinking fund to save for his daughter’s higher studies. At the end of 10 years, he has received an amount of Rs. 10,21,760. What amount did he put in the sinking fund at the end of every 6 months for the tenure, which paid him 5% p.a. compounded semi-annually? [Use (1.025)20= 1.6386]
SECTION – D
(All questions are compulsory. In case of internal choice, attempt any one question only)
32. known that 3% of plastic buckets manufactured in a factory are defective. Using the Poisson distribution on a sample of 100 buckets, find the probability of:
(i) Zero defective buckets
(ii) At most one bucket is defective
[Use 𝑒−3=0.049]
OR
In a math aptitude test, student scores are found to be normally distributed having mean as 45 and standard deviation 5. What percentage of students have scores -
(i) more than the mean score?
(ii) between 30 and 50?
33. An event management company charges Rs. 4,800 per guest, for a bulk booking for 100 guests. In addition, it offers a discount of Rs. 200 for each group of 10 guests over and above 100 guest booking. What is the number of guests that will maximise the amount of money the company receives on a booking? What is the maximum profit on such booking?
OR
To manufacture ‘𝑥’ number of dolls, a company’s total cost function C(𝑥) is given by C (𝑥)=100+0.025𝑥2 and the total revenue function R (𝑥) is described as R (𝑥)=5𝑥. Given that C (𝑥) and R (𝑥) are in thousand rupees, what number of dolls shall be manufactured to maximise the profit of the company? What is the maximum profit?
34. Rahul is at the whole sale market to purchase folding tables and chairs, to later sell them at his furniture shop. He has only Rs. 5,760 to spend and his van has space to carry at the most 20 items. A table costs him Rs. 360 and a chair costs Rs. 240. Back at his shop, he plans to sell a table at a profit of Rs. 22 and a chair at a profit of Rs. 18. Given that he can sell all the items that he purchases, how many tables and chairs shall he purchase in order to maximise his profit?
35. The equilibrium conditions for three competitive markets are described as given below, where 𝑝1,𝑝2 and 𝑝3 are the equilibrium price for each market respectively.
𝑝1+2𝑝2+3𝑝3=85
3𝑝1+2𝑝2+2𝑝3=105
2𝑝1+3𝑝2+2𝑝3=110
Using matrix method, find the values of respective equilibrium prices.
SECTION – E
(All questions are compulsory. In case of internal choice, attempt any one question only)
CASE STUDY – I
36. An overhead water tank has three pipes A, B and C attached to it (as shown in figure (II)). The inlet pipes A and B can fill the empty tank independently in 15 hours and 12 hours respectively. The outlet pipe C alone can empty a full tank in 20 hours.

Based on the above information, answer the following questions. Show steps to support your answers.
a) For a routine cleaning of the tank, the tank needs to be emptied. If pipes A and B are closed at the time when the tank is filled to two-fifth of its total capacity, how long will pipe C take to empty the tank completely?
b) How long will it take for the empty tank to fill completely, if all the three pipes are opened simultaneously?
c) On a given day, pipes A, B and C are opened (in order) at 5 am, 8 am and 9 am respectively, to fill the empty tank. In how many hours will the tank be filled completely?
OR
Given that the tank is half-full, only pipe C is opened at 6 AM, to empty the tank. After closing the pipe C and an hour’s cleaning time, tank is filled completely by pipe A and B together. What is the total time taken in the whole process?
CASE STUDY – II
37. When observed over a long period of time, a time series data can predict trend that can forecast increase or decrease or stagnation of a variable under consideration. Such analytical studies can benefit a business for forecasting or prediction of future estimated sales or production.

Mathematically, for finding a line of best-fit to represent a trend, many methods are available. Methods like moving-averages and least-squares squares are some of the techniques to predict such trends.
Mrs. Shamita runs a bread factory and the record of her sales of bakery items for the period of 2015 - 2019 is as follows:
| Year | 2015 | 2016 | 2017 | 2018 | 2019 |
| Sales (in Rs. thousands) | 35 | 42 | 46 | 41 | 48 |
Based on the above information, answer the following questions. Show steps to support your answers.
a) By taking year 2017 as origin, use method of least-squares to find the best-fit trend line equation for Mrs. Shamita’s business. Show the steps of your working.
OR
Demonstrate the technique to fit the best-suited straight-line trend by the method of 3-years moving averages. Also draw the trend line.
b) What are the estimated sales for Mrs. Shamita’s business for year 2022?
c) Mrs Shamita wishes to grow her business to yearly sale of 67400. In which year will she be able to reach her target?
CASE STUDY – III
38. According to an educational board survey, it was observed that class XII students apply at least one to four weeks ahead of colleges application deadline. Let X represent the week when an average student applies ahead of a college’s application deadline and the probability of student to get admission in the college 𝑃(𝑋=𝑥) is given as follows:
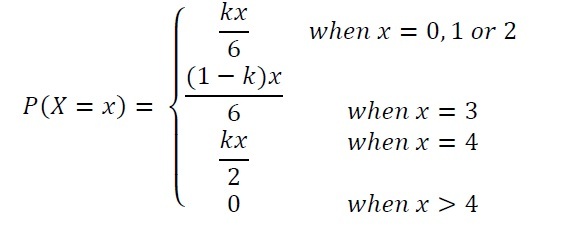
Where k is a real number.
Based on the above information, answer the following questions. Show steps to support your answers.
a) Find the value of k.
b) What is the probability that Sonali will get admission in the college, given that she applied at least 2 weeks ahead of application deadline?
c) Calculate the mathematical expectation of number of weeks taken by a student to apply ahead of a college’s application deadline.
OR
To promote early admissions, the college is offering scholarships to the students for applying ahead of deadline as follows:
Rs. 50000 for applying 4 weeks early,
Rs. 20000 for applying 3 weeks early,
Rs. 12000 for applying 2 weeks early,
and Rs. 9600 for applying 1 week early
What is the expected scholarship offered by the college?
The whole content of the CBSE Class 12 Applied Mathematics Sample Question Paper 2022-23 is given below for easy access.
CBSE Class 12 Applied Mathematics Sample Paper 2022-23 in pdf format to download and print.
Click here to Download - CBSE Class 12 Applied Mathematics Sample Question Paper 2022-23
The marking scheme of the CBSE Class 12 Applied Mathematics Sample Paper 2022-23 in pdf format is attached below.
Click here to Download - CBSE Class 12 Applied Mathematics Marking Scheme 2022-23
Candidates must keep in mind that “The only way to learn Applied Mathematics is to do mathematics.” – Paul Halmos. The only way to excel in the subject is by practising the sums multiple times.
Check your practise below:
| CBSE Class 12 Humanities Practice Papers: All Subjects |
Best of luck to all the candidates.
Comments
All Comments (0)
Join the conversation