CBSE Class 12 Maths Chapter 2 Inverse Trigonometric Functions Revision Notes Download PDF

CBSE Class 12 Mathematics Chapter 2 Inverse Trigonometric Functions Revision Notes: With the 2024 board exams around the corner, the time to lay down the books and begin revising the topics has come. Mathematics is a subject that requires constant practice and thorough revision. In the last stage of the session year, it’s advised to students to focus on revision instead of learning new concepts.

The CBSE Class 12 exams will begin from February 15, 2024, and the mathematics paper is scheduled on March 9. The second chapter in the Class 12 math books is Inverse Trigonometric Functions. It’s an important chapter in the curriculum and holds a substantial weightage in the final exam. You can check out the CBSE Class 12 Chapter 2 Inverse Trigonometric Functions revision notes here, along with supporting study material like mind maps and multiple choice questions.

CBSE Class 12 Maths Chapter 2 Inverse Trigonometric Functions Revision Notes

Basic Definitions and Summary:

Inverse trigonometric functions are the inverse functions of the basic trigonometric functions which are sine, cosine, tangent, cotangent, secant and cosecant.

sin^-1x should not be confused with (sinx)^-1 and the same rule applies to other trigonometric functions.

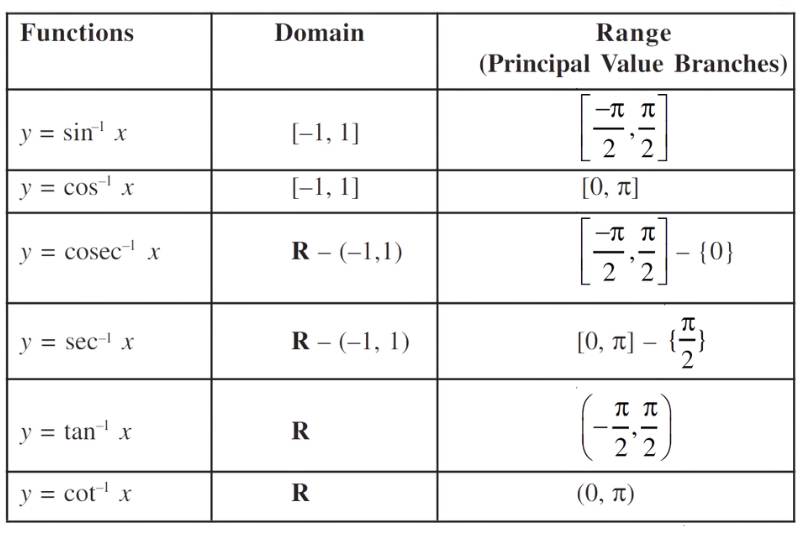
Principal Value: The range of an inverse trigonometric function is the principal value branch and those values which lie in the principal value branch is called the principal value of that inverse trigonometric function.

Whenever no branch of an inverse trigonometric function is mentioned, we mean the principal value branch of that function.

Inverse Trigonometric Formulas

For suitable values of domain, we have

y = sin^-1 x ⇒ x = sin y

x = sin y ⇒ y = sin^-1 x

sin (sin^-1 x) = x

sin^-1 (sin x) = x

Other Formulas:

cos^-1x = π - cos^-1x

tan^-1(-x) = -tan^-1x

cosec⁻¹(-x) = -cosec⁻¹x

sec^-1(-x) = π - sec^-1x

cot^-1(-x) = π - cot^-1x

sin^-1x + cos^-1x = π/2

tan^-1x + cot^-1x = π/2

sec^-1x + cosec^-1x = π/2

Although the syllabus has been rationalized, the following concepts and formulas may benefit students who want to learn a little extra.

sin^-1(1/x) = cosec^-1x, if x ≥ 1 or x ≤ -1

cos^-1(1/x) = sec^-1x, if x ≥ 1 or x ≤ -1

tan^-1(1/x) = cot^-1x, x > 0

sin^-1x + cos^-1x = π/2, x ∈ [-1,1]

tan^-1x + cot^-1x = π/2, x ∈ R

sec^-1x + cosec^-1x = π/2, x ∈ R - [-1,1]

Double Of Inverse Trigonometric Functions

2tan^-1x = sin^-1(2x/1+ x²)

= cos^-1(1-x²/1+x²)

= tan^-1(2x/1-x²)

2sin^-1x = sin^-1(2x.√(1 - x²))

2cos^-1x = cos^-1(2x² - 1)

Triple Of Inverse Trigonometric Functions

3sin^-1x = sin^-1(3x - 4x³)

3cos^-1x = cos^-1(4x³ - 3x)

3tan^-1x = tan^-1(3x - x³/1 - 3x²)

Practise Questions:

1. Find the principal value of cot^-1(-1/√3)

Solution:

Let cot^-1(-1/√3) = y. Then,

coty = -1/√3 = -cot (π/3) = cot 3 (π-π/3) = cot (2π/3)

We know that the range of principal value branch of cot ^-1 is (0, π) and (cot 2π/3) = (-1/√3)

Hence, principal value of cot^-1(-1/√3) is 2π/3

2. sin[π/3 – sin-1(-½)] is equal to:

Solution:

sin[π/3 – sin^-1(-½)]

= sin[π/3 – sin^-1[sin (-π/6))]

sin[π/3 – (-π/6)]

= sin(π/3 + π/6)

= sin π/2

= 1

3. If tan^-1(√3) + cot^-1x = π2‚ then find the value of x. (All India 2010C)
   Solution:

Given, tan^-1 √3 + cot^-1 x = π2
⇒ tan^-1 √3 = π2 – cot^-1 x
⇒ tan^-1 √3 = tan^-1 x
[∵ tan^-1 x + cot^-1 x = π2; x ∈ R]
∴ x = √3

Recommended:

NCERT Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions

MCQs for CBSE Class 12 Maths Chapter 2 Inverse Trigonometric Functions

CBSE Inverse Trigonometric Functions Class 12 Mind Map for Chapter 2 of Maths, Download PDF

CBSE Class 12 Maths Chapter 2 Inverse Trigonometric Functions Formulas List