Maths Integrals Formulas: The CBSE Class 12 mathematics course is heavily focused on calculus, and Chapter 7 Integrals is one of the lengthiest and most important chapters on the topic. Integrals is the first chapter in book 2 and covers the branch of calculus that deals with finding out the numerical values of the area under the graph of a function for some interval.
Integration is the opposite of derivation and one of the two fundamental operations in calculus, making Integrals essential from an exam perspective and application in higher studies as well. Integrals consist of numerous formulas, theorems, identities and rules that students need to learn.
Learning formulas helps simplify complex equations and solve problems quickly. On that note, be sure to take a look at the CBSE Class 12 Maths Chapter 7 Integrals Formulas below.
Recommended:
CBSE Class 12 Maths Mind Map for Chapter 7 Integrals
CBSE Class 12 Maths Chapter 7 Integrals MCQs
CBSE Class 12 Maths Chapter 7 Integrals Formulas and Theorems
We have listed all the important formulas, definitions and properties of CBSE Class 12 Integrals here.
Integration
In differential calculus, we are given a function and we have to find the derivative or differential of this function, but in integral calculus, we are to find a function whose differential is given. Thus, integration is a process which is the inverse of differentiation.
Definite Integrals
A definite integral is the area under a curve between two fixed limits.
Properties of Definite Integrals

Indefinite Integrals
An integral which is not having any upper and lower limit.
First fundamental theorem of integral calculus
Let the area function be defined by A(x) = a∫x ƒ(x)dx for all x ≥ a, where the function ƒ is assumed to be continuous on [a, b]. Then A′(x) = ƒ (x) for all x ∈ [a, b].
Second fundamental theorem of integral calculus
Let ƒ be a continuous function of x defined on the closed interval [a, b] and let F be another function such that d/dx F(x) = ƒ(x) for all x in the domain of ƒ, then
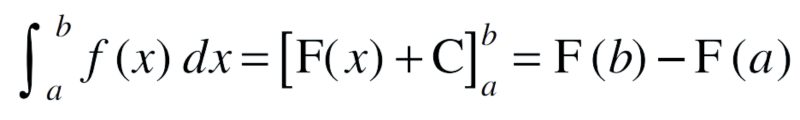
This is called the definite integral of ƒ over the range [a, b], where a and b are called the limits of integration, a being the lower limit and b the upper limit.
Standard Integrals

Integration By Substitution
A change in the variable of integration often reduces an integral to one of the fundamental integrals. The method in which we change the variable to some other variable is called the method of substitution. When the integrand involves some trigonometric functions, we use some well-known identities to find the integrals. Using the substitution technique, we obtain the following standard integrals.
(i) ∫tanxdx = log|secx|+ C
(ii) ∫cotxdx = log|sinx|+ C
(iii) ∫secxdx= log|secx + tanx|+ C
(iv) ∫cosecxdx = log|cosecx - cotx|+ C
Also Read
CBSE Class 12 Maths Syllabus 2023-24
CBSE Class 12 Maths Sample Paper 2023-24
NCERT Solutions for Class 12 Maths PDF
Comments
All Comments (0)
Join the conversation