Angular Velocity Formula: The explainer provided here is for the angular velocity that covers its meaning, definition, formula, examples, its relation with linear velocity, etc. To get a school-level understanding of angular velocity refer to this concept explainer.
What is Angular Velocity?
Angular velocity is a measure of how quickly an object rotates or revolves around a central point or axis. It is a vector quantity, meaning it has both a magnitude and a direction.
Angular Velocity Definition
Angular velocity (ω) is defined as the rate of change of angular displacement with respect to time. It describes how fast an object is rotating and in which direction.
Angular Velocity Formula
The formula for angular velocity is given by: ω=Δθ/Δt where:
- ω = angular velocity (radians per second)
- Δθ = change in angular displacement (radians)
- Δt = change in time (seconds)
Average Angular Velocity
Average angular velocity is the total angular displacement divided by the total time taken: ωavg=θfinal−θinitial/tfinal−tinitial
It provides a measure of how fast an object rotates over a specified period of time.
Instantaneous Angular Velocity
Instantaneous angular velocity is the angular velocity at a specific moment in time. It is found by taking the limit of the average angular velocity as the time interval approaches zero: ω=limΔt→0Δθ/Δt=dθ/dt
Also Read:
- Avogadro’s Number: Definition, Value, Meaning, Unit and Symbol
- Magnetic Field: Formula, Properties, and Applications
- Archimedes' Principle: Formula, Derivation, Applications and Examples
- Law of Conservation of Energy
Angular Velocity Direction
The direction of angular velocity is given by the axis of rotation and follows the right-hand rule. It is perpendicular to the plane of rotation.
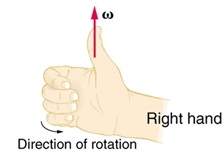
Right Hand Rule
To determine the direction of angular velocity using the right-hand rule, point the thumb of your right hand in the direction of the axis of rotation. Curl your fingers in the direction of rotation. Your thumb points in the direction of the angular velocity vector.
Relationship Between Angular Velocity and Linear Velocity
The relationship between angular velocity (ω) and linear velocity (v) for a point at a distance r from the axis of rotation is v=r⋅ω where:
- v = linear velocity
- r = radius (distance from the axis of rotation)
Angular Velocity Real Life Examples
- Spinning Top: The angular velocity describes how fast the top spins around its axis.
- Ferris Wheel: The angular velocity indicates how quickly the wheel rotates.
Angular Velocity of the Earth
The Earth rotates once about its axis approximately every 24 hours. The angular velocity of the Earth is: ωEarth=2π radians/24×3600 seconds≈7.27×10−5 radians/second
Angular Velocity of the Hour Hand
The hour hand of a clock completes one revolution every 12 hours. The angular velocity of the hour hand is:
ωhour hand=2π radians/12×3600 seconds≈1.45×10−4 radians/second
Angular Velocity of the Wheel
For a wheel with a radius r rotating at N revolutions per minute (RPM), the angular velocity is: ωwheel=2πN/60 radians/second where:
- N = rotational speed in RPM
Calculation Examples on Angular Velocity
Example 1: Calculating the Angular Velocity of a Spinning Top
A top completes 20 rotations in 10 seconds. What is its angular velocity?
Solution:
- Find the angular displacement: Δθ=20 rotations×2π radians/rotation=40π radians
- Find the time interval: Δt=10 seconds
- Use the formula for angular velocity:
ω=Δθ/Δt=40π radians/10 seconds=4π radians/second
The angular velocity of the spinning top is 4π4\pi4π radians per second.
Example 2: Angular Velocity of a Ferris Wheel
A Ferris wheel with a radius of 15 meters completes one full rotation in 30 seconds. What is its angular velocity?
Solution:
- Find the angular displacement: Δθ=2π radians
- Find the time interval: Δt=30 seconds
- Use the formula for angular velocity: ω=Δθ/Δt=2π radians/30 seconds=π/15 radians/second
- The angular velocity of the Ferris wheel is π/15 radians per second.
Example 3: Angular Velocity of a Rotating Wheel
A car’s wheel with a radius of 0.5 meters is rotating at 120 RPM (revolutions per minute). What is its angular velocity in radians per second?
Solution:
- Convert RPM to radians per second:
120 RPM=120×2π radians/60 seconds=4π radians/second
The angular velocity of the car’s wheel is 4π radians per second.
This completes the basic guide on angular velocity which students can refer to as a quick reference material to revise for their exam.
References and Further Reading
You can refer to the reference material provided in the below mentioned links for better preparation and understanding scientific concepts.
- Books
NCERT Class 10 Science Textbook PDF
NCERT Class 12 Physics Textbook PDF
- Articles
Magnetic effects of Electric Current
- Online Resources
CBSE Class 10 Science Video Tutorials
CBSE Class 12 Physics Video Tutorials
Also Check:
Comments
All Comments (0)
Join the conversation