Determinants and Matrices: Concepts, Definition and Types

In the realm of linear algebra, determinants and matrices are essential tools used to solve systems of linear equations, especially when applying Cramer's rule to non-homogeneous linear equations. Determinants are exclusively computed for square matrices. A determinant is considered singular if its value is zero, and unimodular if it equals one. For a system of equations to have a unique solution, the matrix's determinant must be nonsingular, indicating it is non-zero. This article delves into the definitions of determinants and matrices, explores various matrix types, discusses their properties, and provides practical examples.

Definition of Matrices 

Matrices are structured rectangular arrays of numbers used to represent linear equations. They consist of rows and columns, enabling mathematical operations like addition, subtraction, and multiplication. A matrix with m rows and n columns is denoted as an m × n matrix.

Types of Matrices

There are different types of matrices. Let’s see some of the examples of different types of matrices

Definition of Determinant

A determinant can be defined in various ways for a square matrix. One straightforward method involves using the elements of the first row and their corresponding minors. Start by multiplying the first element of the top row by its minor, then subtract the product of the second element and its minor. Continue this alternating addition and subtraction process for each element of the top row until all elements have been processed.

For example let us consider a 4×4 matrix A.

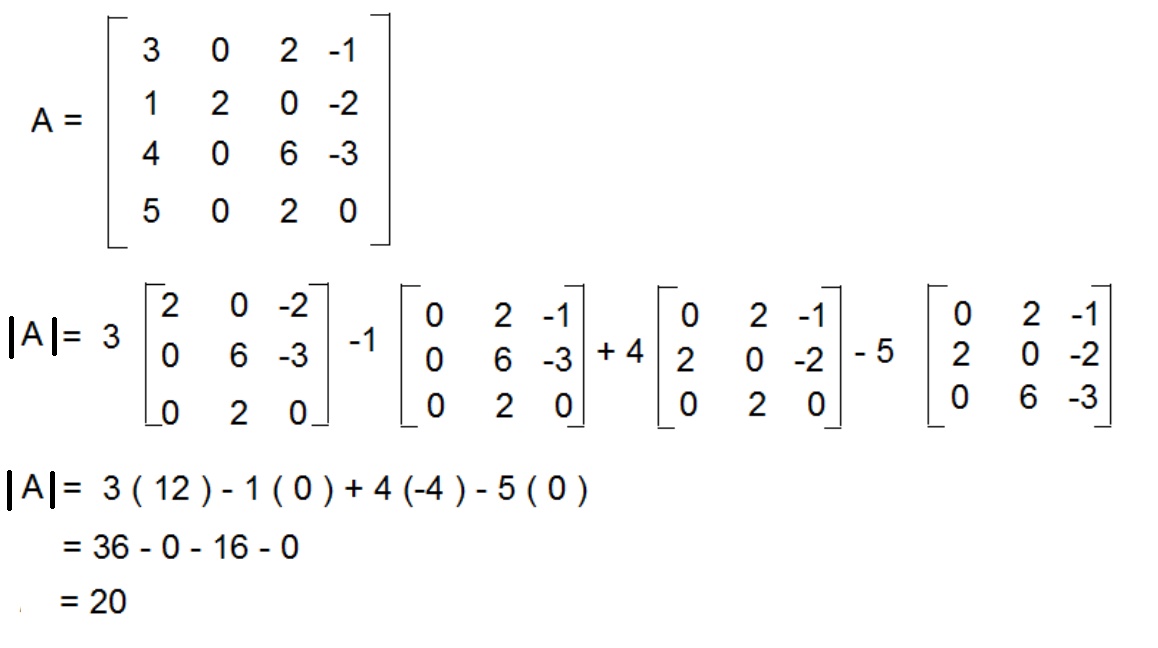
Properties of Determinants

Properties of Determinants: The properties help you solve determinants more efficiently by recognizing patterns and making calculations easier. 

Important Properties of Determinants

• Interchanging the rows and columns of a determinant does not alter its value.
• Interchanging any two rows or columns of a determinant will reverse its sign.
• If any two rows or columns of a determinant are identical, its value will be zero.
• Multiplying any element of a row or column of a determinant by a constant K also multiplies the determinant's value by K.
• If we express some or all elements of a column or row of a determinant as a sum of two or more terms, we can represent the determinant as the sum of two or more determinants.

Check: 

Profit And Loss

Multiplication Tables

Relations and Functions