Key Points
- Fractions are a foundational concept in mathematics, essential for understanding parts of a whole.
- Fractions help learn ratios, percentages, and algebra better.
- Dividing pizza is a practical example of using fractions to share equal parts.
Fractions are an essential concept in mathematics used to represent parts of a whole. They express a number that is not whole, breaking down values into smaller, equal parts. Here’s a breakdown of fractions, along with simple definitions, types, and examples:
Definition of a Fraction: A fraction represents a part of a whole and is written in the form of a/b, where a is called the numerator and b is called the denominator.
Parts of Fraction
- Numerator (a): The top part of the fraction, indicating how many parts are being considered is the numerator of the fraction.
- Denominator (b): The bottom part, showing the total number of equal parts the whole is divided into is the denominator of the fraction.
Types of Fractions
1. Proper Fractions: These are the fractions where the numerator is smaller than the denominator. For example, 3/4. These are always less than 1.
2. Improper Fractions: Fractions where the numerator is equal to or greater than the denominator are termed as improper fractions. For example, 5/3. These can be converted to mixed numbers.
3. Mixed Fraction: A whole number combined with a proper fraction makes a mixed fraction.
4. Equivalent Fractions: Fractions that represent the same value, even if the numerators and denominators are different are called equivalent fractions. For example, 1/2=2/4=3/6.
5. Unit Fraction: Fractions in which the numerator is 1 is called the unit fraction. For example, 1/4, 1/7, 1/9, etc.
Operations with Fractions
- Addition/Subtraction: To add or subtract, convert fractions to a common denominator, then perform the operation on the numerators.
- Multiplication: Multiply the numerators together and the denominators together. For example, 1/2×3/4=3/8
- Division: Invert the second fraction (reciprocal) and multiply. For example, 1/2÷3/4=1/2×4/3=2/3
- Simplifying Fractions: Divide the numerator and the denominator by their greatest common factor (GCF) to express the fraction in its simplest form.
Real-Life Examples of Fractions
There are several instances in daily life where fractions are used to simplify or represent parts of a whole. Some common examples include:
- Cooking: Ingredients are often measured in fractions, such as 1/2 cup of sugar or 3/4 tablespoon of salt.
- Pizza Slices: When we divide a pizza into 4 equal parts, then each part is 1/4th of the whole.
- Construction: Fractions are crucial when measuring materials for construction. Example. cutting wood to 3/4 of an inch.
- Shopping: Fractions are used to calculate discounts, such as when a sweater is on sale for 25% off.
- Eating out: Fractions are used to divide the bill at a restaurant.
- Medicine: Doctors prescribe different dosages of medication based on fractions.
- Mocktails: Fractions are used to mix different liquids in the right amounts to make mocktails.
- Test scores: Test and exam scores are often expressed as fractions.
Fractions are fundamental in everyday situations and lay the groundwork for more complex math concepts, such as ratios, percentages, and proportions. The foundational understanding of fundamentals can help students grasp fractions better and recognize their applications in daily life, making the subject both practical and relevant.
Fractions Practice Questions
Q.Write the fraction representing the shaded portion in the following images:
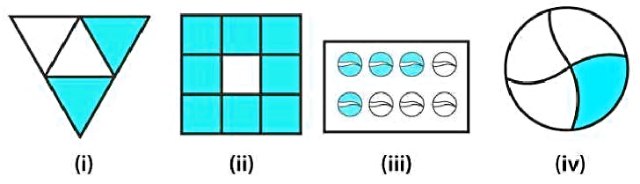
Answer:
(i)2/4
(ii)8/9
(iii)4/8
(iv)1/4
Q. The numerator of a fraction is 4 less than its denominator. If the numerator is decreased by 2 and denominator is increased by 1, then the denominator becomes 8 times the numerator, find the fraction.
Answer: 3/7
Q. Find the two fractions that are equivalent to 3/7.
Answer: 3/7 = 6/14 and 3/7 = 9/21
Also Check:
Probability Notes: Definition, Types, Formulas, Applications and More
Comments
All Comments (0)
Join the conversation