Pythagoras Theorem: Definition, Formula, Proof, Examples and Applications

Pythagoras Theorem: The Pythagoras Theorem is a fundamental principle in geometry, attributed to the ancient Greek mathematician Pythagoras. This theorem establishes a relationship between the sides of a right-angled triangle. Pythagoras Theorem explains the relationship between the three sides of a right-angled triangle and helps us find the length of a missing side if the other two sides are known.

It is also known as the Pythagorean theorem.

Pythagoras Theorem Definition

The Pythagoras Theorem states that in any right-angled triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the other two sides (a and b).

Pythagoras Theorem Formula

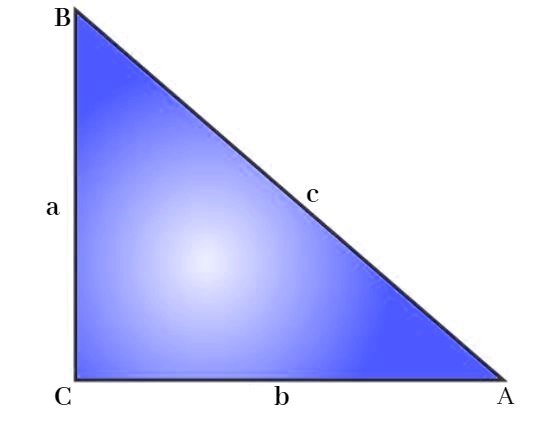
Let us take

• Altitude = a
• Base = b
• Hypotenuse = c

The Pythagoras Theorem formula is given as:

c² = a² + c²

where:

• a and b are the lengths of the two sides of the right-angled triangle.
• c is the length of the hypotenuse, which is the side opposite the right angle.

The Pythagoras theorem can apply to any triangle with one angle equal to 90 degrees.

Proof of Pythagoras Theorem 

Here’s a simple proof of Pythagoras Theorem using similar triangles:

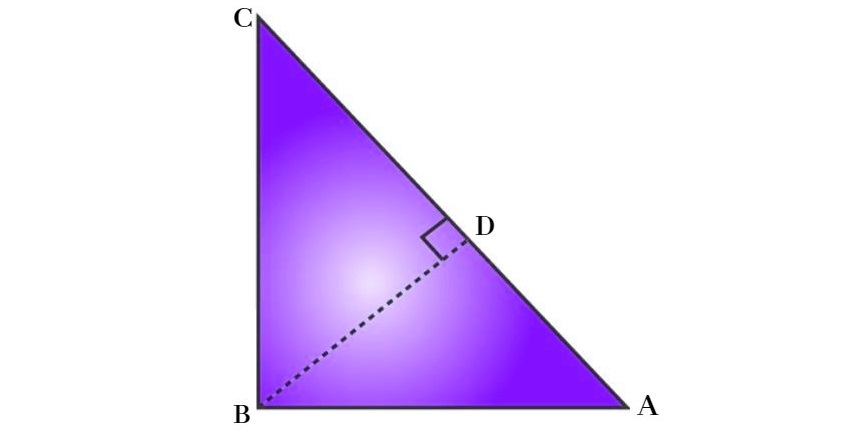
In △ABD and △ACB,

∠A = ∠A           (Common angle)

∠ADB = ∠ABC = 90°

Therefore, we can say △ABD ∼ △ ACB (By AA Similarity)

Similarly, △BDC ∼ △ACB

Hence, AD/AB = AB/AC gives

AB² = AD × AC      ………….(1)

And, CD/BC = BC/AC gives

BC² = CD × AC       ………….(2)

Adding equations (1) and (2),

AB² + BC² = AC × AD + AC × CD

AB² + BC² = AC (AD + CD)

AB² + BC² = AC × AC

AB² + BC² = AC²

Or AC² = AB² + BC²

Hence proved.

Converse of Pythagoras Theorem

The converse of Pythagoras theorem states that if the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.

Proof of Converse of Pythagoras Theorem

Given a triangle with sides of length a, b, and c, if a² + b² = c², then the angle between sides a and b is a right angle.

Proof:

Let ABC be a triangle with side lengths a, b, and c.

We assume that it satisfies c² = a² + b^2.

Construct a second triangle △EFG with sides of length a and b containing a right angle.

Thus, AC = EG = b and BC = FG = a

By applying Pythagoras Theorem in △EFG, we get 

⇒ EF² = EG² + FG² = b² + a²    ………………(1)

In △ABC, Given that:

c² = a² + b^2.

⇒ AB² = AC² + BC² = b² + a²      ………………(2)

From equations (1) and (2), we have;

⇒ EF² = AB²

⇒ EF = AB

Now, in ΔABC and ΔEFG,

AC = EG (By construction)

BC = FG (By construction)

AB = EF (Proved)

So, ΔABC ≃ ΔEFG (According to the SSS congruence)

∠C = ∠G (Corresponding angles of congruent triangles)

∠G = 90° (By construction)

So ∠C = 90°.

Hence, the converse of the Pythagoras theorem is proved.

Applications of Pythagoras Theorem

The Pythagoras Theorem has numerous applications in various fields such as:

• Geometry: Calculating distances between points, finding the length of sides in triangles, and solving problems involving polygons.
• Trigonometry: Used for defining trigonometric ratios like sine, cosine, and tangent.
• Physics: Analyzing forces, motion, and vectors.
• Engineering: Designing and constructing buildings, bridges, and other structures.
• Navigation: Determining shortest paths and distances between locations.

Pythagoras Theorem Solved Examples

1.Given a right-angled triangle with sides a = 3 units and b = 4 units, find the hypotenuse c.

Solution:

Using the Pythagoras Theorem:

c²=3²+4²

⇒ c²=9+16

⇒ c²=25

⇒ c = √25

⇒ c = 5

2.Given a right-angled triangle with hypotenuse c = 10 units and one side, a = 6 units, find the other side of the triangle.

Solution:

Using the Pythagoras Theorem or given triangle we get:

10² = 6² + b²

⇒ 100 = 36 + b²

⇒ b² = 100 − 36

⇒ b² = 64

⇒ b =  √64 = 8

⇒ B = 8

Conclusion

The Pythagoras Theorem is a fundamental principle in mathematics that provides a powerful tool for solving problems involving right-angled triangles. Its wide range of applications makes it an essential concept in both theoretical and applied mathematics.

Also Read

• NCERT Book for Class 10 Maths
• NCERT Solutions for Class 10 Maths

Video Courses for PCMB (Class 10 and 12)

You can now access video lectures designed by experts for major topics of Physics, Chemistry, Maths and Biology to get a better concept clarity and achieve success in your academics. Find the video link below:

• CBSE  Class 10 Video Courses for Board Exams 2025
• CBSE  Class 12 Video Courses for Board Exams 2025