Maths Three Dimensional Geometry Formulas: The class 12 mathematics course is predominantly calculus based but there are other chapters that hold significant importance and marks weightage in exams.
The Class 12 NCERT Chapter 11 Three Dimensional Geometry is a unique topic and requires substantial effort from students. It combines concepts of vectors, coordinate geometry, trigonometry and matrices.
As such, your fundamental knowledge of maths must be on point before you begin 3-D Geometry. The chapter is essential from an exam perspective as well and one of the lengthiest in the curriculum.
There are multiple formulas, rules and definitions that students have to learn in Three Dimensional Geometry, and we’re here to help you in that task. The NCERT has rationalized the books, and CBSE has reduced the syllabus for Class 12 students.
However, we have listed both the necessary and deleted formulas so high achievers, and engineering aspirants can also avail the benefits. Check the CBSE Class 12 Maths Chapter 11 Three Dimensional Geometry Formulas below.
Recommended:
CBSE Class 12 Maths Mind Map for Chapter 11 Three Dimensional Geometry
CBSE Class 12 Maths Chapter 11 Three Dimensional Geometry MCQs
CBSE Class 12 Maths Chapter 11 Three Dimensional Geometry Formulas and Theorems
We have listed all the important formulas, definitions and properties of CBSE Class 12 Three Dimensional Geometry here.
- The direction cosines of a line are the cosines of the angles made by the line with the positive directions of the coordinate axes.
- If l, m, n are the direction cosines of a line, then l2+ m2 + n2 = 1.
- Direction cosines of a line joining two points P ( x1 , y1 , z1 ) and Q ( x2, y2 , z2 ) are:
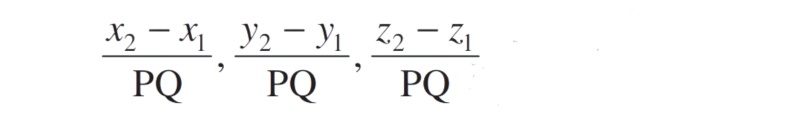
Where PQ = √(x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2
- The direction ratios of a line are the numbers which are proportional to the direction cosines of a line.
- If l, m, n are the direction cosines and a, b, c are the direction ratios of a line then
l = a/√a2 + b2 + c2 ;
m = b/√a2 + b2 + c2
n = c/√a2 + b2 + c2
- Skew lines are lines in space which are neither parallel nor intersecting. They lie in different planes.
- The angle between skew lines is the angle between two intersecting lines drawn from any point (preferably through the origin) parallel to each of the skew lines.
- If l1, m1 , n1 and l2 , m2 , n2 are the direction cosines of two lines; and θ is the acute angle between the two lines; then
cosθ = |l1 l2 + m1m2 + n1 n2 |
- If a1, b1 , c1 and a2 , b2 , c2 are the direction ratios of two lines and θ is the acute angle between the two lines; then
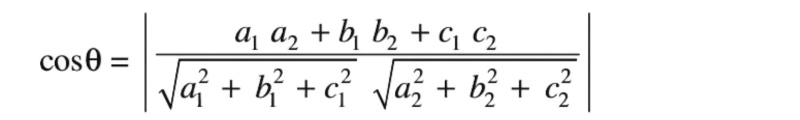

- Equation of a line through a point (x1, y1, z1 ) and having direction cosines l, m, n is (x-x1)/l = (y-y1)/m = (z-z1)/n
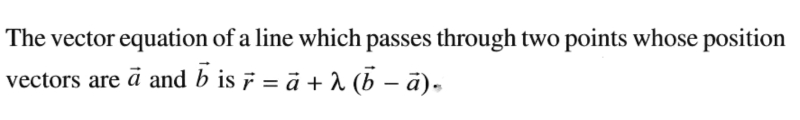
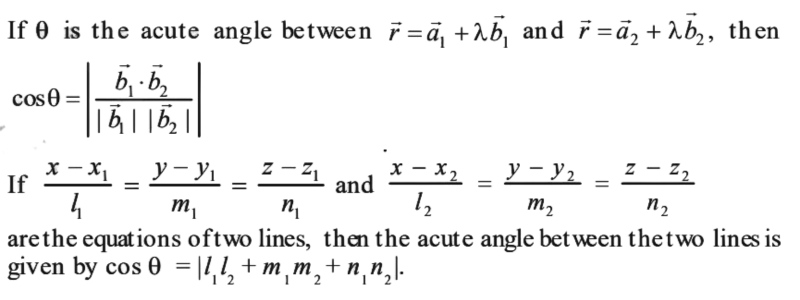
- The shortest distance between two skew lines is the line segment perpendicular to both lines.
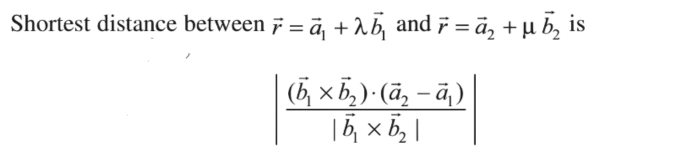

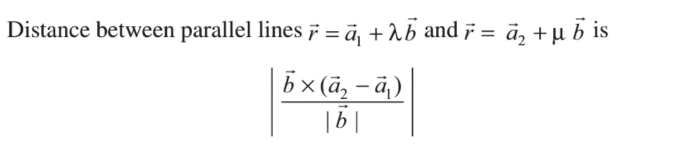
Also Read
CBSE Class 12 Maths Syllabus 2023-24
CBSE Class 12 Maths Sample Paper 2023-24
NCERT Solutions for Class 12 Maths PDF
Comments
All Comments (0)
Join the conversation