AP Inter 1st Year Mathematics 1A Exam 2025:Candidates can find a detailed exam analysis for the AP Inter 1st Year Mathematics 1A exam on this page. The exam ended at 12 PM. This analysis includes the overall difficulty level of the paper and the difficulty level of each section – Section A, Section B, and Section C.
It will also provide an idea of the expected good score, helping students assess their performance. Additionally, student reviews and feedback will be collected and updated here. These reviews will give valuable insights into the question paper, helping students understand the exam better.
AP Inter 1st Year Mathematics 1A Question Paper 2025

Download the question paper for 1st Year AP Inter Maths 1A 2025 exam here:
AP Inter 1st Year Mathematics 1A Question Paper 2025 Download PDF |
AP Inter 1st Year Mathematics 1A Exam Analysis 2025
Here is the AP Inter 1st Year Mathematics 1A Exam Analysis 2025 in a tablulated information:
| Particulars | Details |
|---|---|
| Overall difficulty level of the exam | Moderate |
| Complexity level of Section A | Moderate to Challenging |
| Complexity level of Section B | Moderate |
| Complexity level of Section C | Easy to Moderate |
| Was the exam time-consuming? | Yes, slightly lengthy |
| Expected good score | To Be Updated |
AP Inter 1st Year Maths 1A Answer Key 2025
The answer key for the AP Inter 1st Year Mathematics 1A exam is available now. Students can check the correct answers and evaluate their performance in exam. Check answers and solutions below:
1.Find the domain of the real valued function f(x) = 1/√(1 - x2).
Answer: The domain of the function will be [−1,1].
2.If A = {1,2,3,4} and f: A →R is a function defined by f(x) = (x2 - x + 1)/ (x+1) = 1, then find the range of f.
Solution: Given A={1,2,3,4}
f:A→R such that f(x)=(x2 - x + 1)/(x+1)
f(1)=(12 - 1 + 1)/ (1+1) = 1/2
f(2)=(22 - 2 + 1)/ (2+1) = (4−2+1)/3 = 3/3 = 1
f(3)=(32−3+1)/(3+1) = (9−3+1)/4 = 7/4
f(4) = (42−4+1)/(4+1) = (16−4+1)/5 = 13/5
∴ Range of f={1/2,1,7/4,13/5}
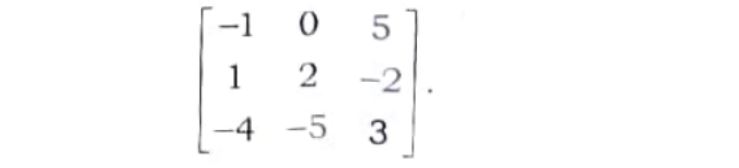
3. Find the co-factors of the elements 2 and -5 in the matrix,
Answer:
Co-factor of 2 = 17
Co-factor of -5 = 3
4.
Answer:
x = 2, y = 2, z = 5 and a = 5
5. Find a vector in the direction of vector a = i - 2j that has magnitude 7 units.
Answer:
The, required vector is :
6. Find the vector equation of the line joining the points 2i+ j+3k and -4i+3j-k.
Answer:
The required vector equation is, r = (1 - t) (2i + j + 3k) + t(-4i + 3j - k)
7. Find the angle between the planes r. (2i - j + 2k) = 3 and r. (3i + 6j + k) = 4.
Answer:
Required angle is, θ = cos-1(2/∛46)
8. Find the maximum and minimum value of 3 sinx - 4cosx.
Answer:
Maximum value = 5
Minimum value = -5
We are updating more answers, keep refreshing this page.

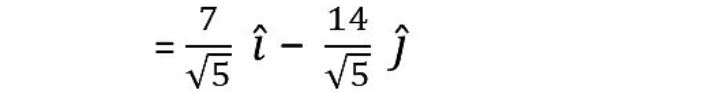
Comments
All Comments (0)
Join the conversation