CBSE Class 12 Applied Mathematics Syllabus 2021-22 (New): CBSE Academic Session 2021-22

Check CBSE Class 12 Applied Mathematics Syllabus 2021-22 and prepare for upcoming CBSE Class 12 Applied Mathematics board exam.

Mayank Uttam

Updated: May 5, 2021 08:42 IST

CBSE 2021-22

Check CBSE Class 12 Applied Mathematics Syllabus 2021-22. The link to download CBSE Class 12 Applied Mathematics Syllabus 2021-22 is given at the end of this article. Download now and prepare for CBSE Class 12 Applied Mathematics board exam.

New CBSE Syllabus 2021-22 (PDF) for 9th, 10th, 11th, 12th: CBSE Curriculum 2021-22 Applicable for CBSE Academic Session 2021-22

CBSE Class 12 Applied Mathematics Syllabus 2021-22:

Total number of Periods: 240 (35 Minutes Each)

Number of Paper: 1

Time: 3 Hours

Max Marks: 80

No.	Units	No. of Periods	Marks
I	Numbers, Quantification and Numerical Applications	30	09
II	Algebra	20	10
III	Calculus	50	15
IV	Probability Distributions	35	10
V	Inferential Statistics	10	05
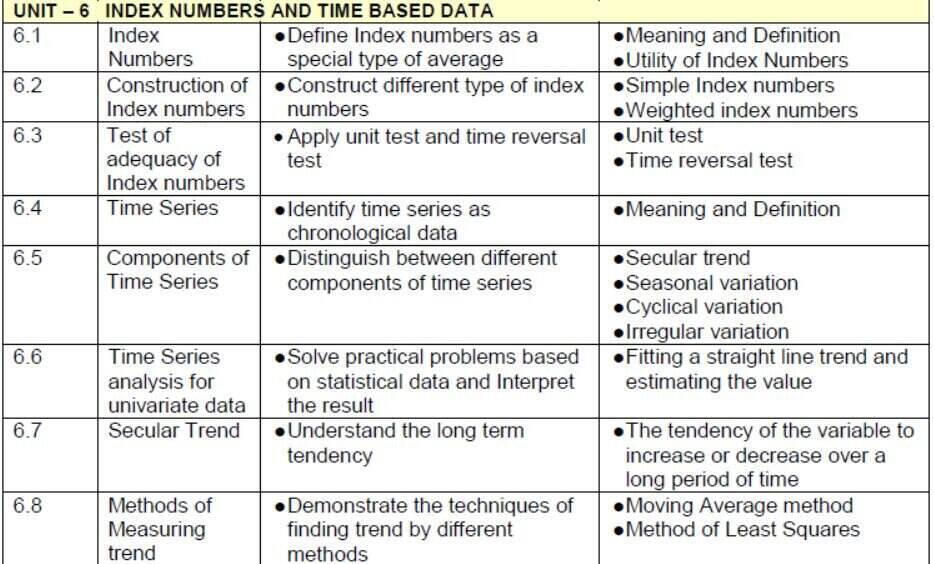
VI	Index Numbers and Time-based data	30	10
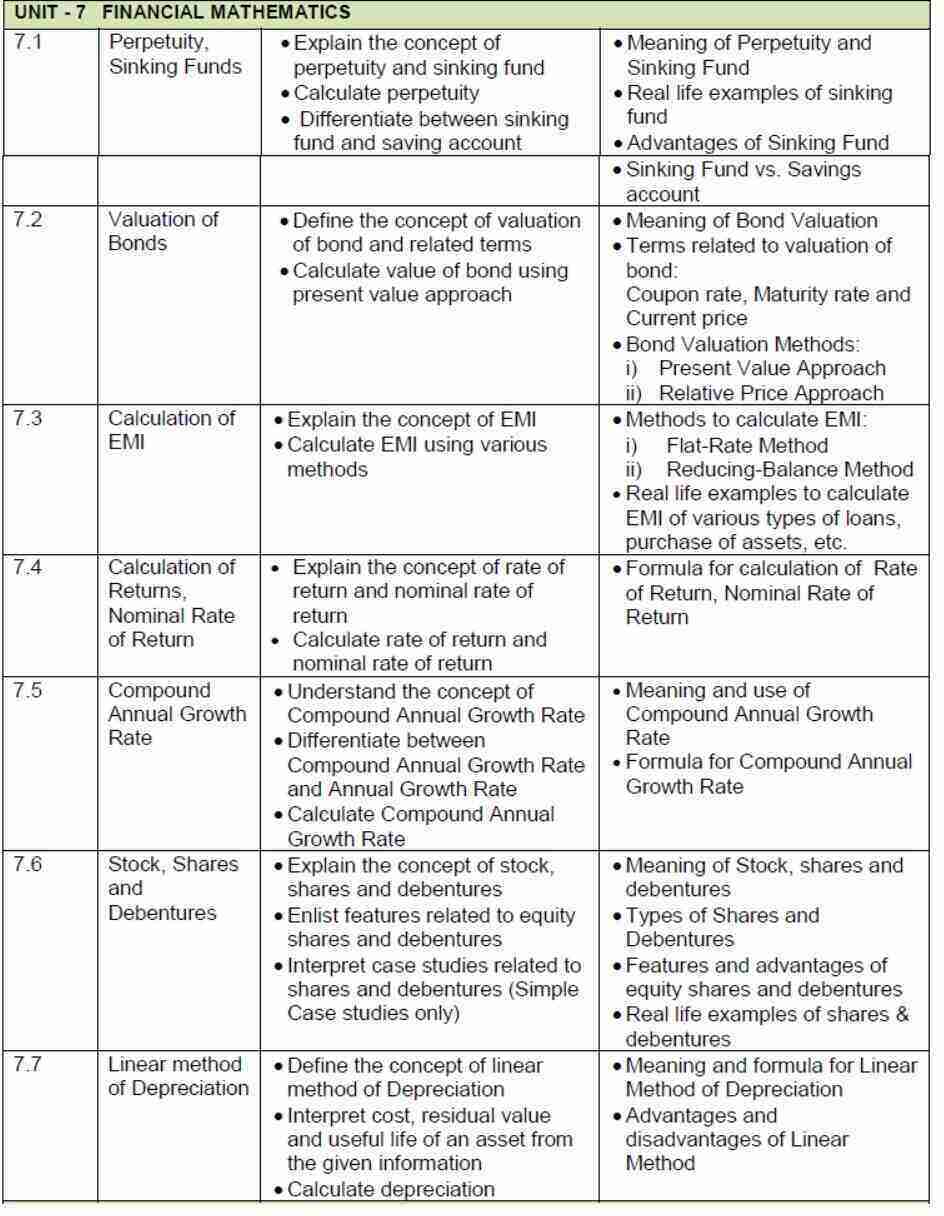
VII	Financial Mathematics	50	15
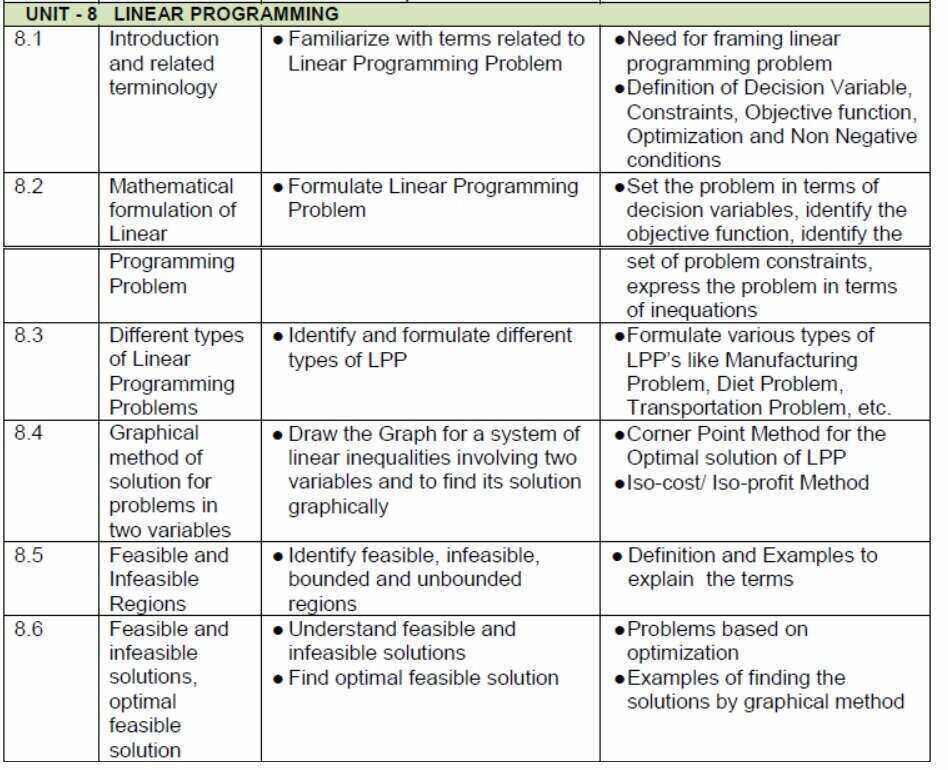
VIII	Linear Programming	15	06
Total		240	80
Internal Assessment		20

CLASS XII

Sl. No.

Contents

Learning Outcomes: Students will be able to

Notes / Explanation

UNIT-1 NUMBERS, QUANTIFICATION AND NUMERICAL APPLICATIONS

1.1

Modulo

Arithmetic

· Define modulus of an integer

· Apply arithmetic operations using modular arithmetic rules

· Definition and meaning

· Introduction to modulo operator

· Modular addition and subtraction

1.2

Congruence

Modulo

●Define congruence modulo

●Apply the definition in various

problems

●Definition and meaning

●Solution using congruence

modulo

●Equivalence class

1.3

Simple

Arithmetic

Functions

· Define arithmetic function

· Enlist different arithmetic functions

· Apply the arithmetic functions on given number

Properties and Examples of:

i) Euler totient function

ii) Number of divisor function iii) Divisor sum function

iv) Mobius function

1.4

Alligation and

Mixture

●Understand the rule of alligation to produce a mixture at a given price

●Determine the mean price of a mixture

●Apply rule of alligation

●Meaning and Application of rule of alligation

●Mean price of a mixture

1.5

Numerical

Problems

Solve real life problems mathematically

Boats and

Streams

(upstream and downstream)

●Distinguish between upstream and downstream

●Express the problem in the form of an equation

● Problems based on speed of stream and the speed of boat in still water

Pipes and

Cisterns

●Determine the time taken by two or more pipes to fill or empty the tank

●Calculation of the portion of the tank filled or drained by the pipe(s) in unit time

Races and

Games

●Compare the performance of two players w.r.t. time, distance

●Calculation of the time taken/ distance covered / speed of each player

Partnership

●Differentiate between active partner and sleeping partner

●Determine the gain or loss to be divided among the

partners in the ratio of their

investment with due consideration of the time

●Definition, Profit division among the partners

Scheduling

●Define scheduling

●Differentiate between FCFS &

SJF

●Solve problems based on FCFS and SJF

●Definition and meaning

●Use of Gantt chart

Simple problems based on

FCFS (First come First serve) and SJF (shortest job first)

1.6

Numerical

Inequalities

●Describe the basic concepts of numerical inequalities

●Understand and write numerical inequalities

●Comparison between two statements/situations which can be compared numerically

●Application of the techniques of numerical solution of algebraic inequations

UNIT-2 ALGEBRA

2.1

Matrices and types of matrices

● Define matrix

● Identify different kinds of

matrices

● Find the size / order of matrices

● The entries, rows and columns of matrices

● Present a set of data in a matrix form

2.2

Equality of

matrices, Transpose of a matrix, Symmetric and Skew symmetric matrix

· Determine equality of two matrices

· Write transpose of given matrix

· Define symmetric and skew symmetric matrix

· Examples of transpose of matrix

· A square matrix as a sum of symmetric and skew symmetric

matrix

· Observe that diagonal elements of skew symmetric matrices are always zero

2.3

Algebra of

Matrices

● Perform operations like addition

& subtraction on matrices of

same order

● Perform multiplication of two matrices of appropriate order

● Perform multiplication of a scalar with matrix

● Addition and Subtraction of matrices

● Multiplication of matrices (It can be shown to the students that Matrix multiplication is

similar to multiplication of two

polynomials)

● Multiplication of a matrix with a real number

2.4

Determinants

● Find determinant of a square matrix

● Use elementary properties of determinants

● Singular matrix, Non singular matrix

● |AB|=|A||B|

● Simple problems to find

determinant value

2.5

Inverse of a

matrix

· Define the inverse of a square matrix

· Explain elementary row operations and use to it find the

inverse of a matrix

· Apply properties of inverse of matrices

· Inverse of a matrix using:

a) cofactors

b) elementary row operations

· If A and B are invertible square matrices of same size,

i) (AB)-1=B -1A –1

ii) (A-1)-1 =A

iii) (AT)-1 = (A-1)T

2.6

Solving system of

simultaneous

equations using matrix method, Cramer’s rule and row reduction method

· Solve the system of simultaneous equations using

i) Cramer’s Rule

ii) Inverse of coefficient matrix iii) Row reduction method

· Formulate real life problems into a system of simultaneous linear equations and solve it

using these methods

· Solution of system of simultaneous equations upto

three variables only

(non- homogeneous equations)

2.7

Simple

applications of matrices and determinants including Leontiff input output model for two variables

· Apply simple applications of matrices and determinants in different areas of mathematics,

physics, coding, encryption etc.

· Apply real life applications particularly for Leontiff input output model for two variables

in economics

· Real life applications of

Matrices and Determinant

· Leontiff Input–output model that represents the interdependencies between different sectors of a national economy or different regional economies

UNIT- 3 CALCULUS

Differentiation and its Applications

3.1

Higher Order

Derivatives

· Determine second and higher order derivatives

· Understand differentiation of parametric functions and

implicit functions

· Simple problems based on higher order derivatives

· Differentiation of parametric functions

and implicit functions (upto

2nd order)

3.2

Application of

Derivatives

· Determine the rate of change of various quantities

· Understand the gradient of tangent and normal to a curve at a given point

· Write the equation of tangents and normal to a curve at a given

point

· To find the rate of change of quantities such as area and

volume with respect to time or

its dimension

· Gradient / Slope of tangent and normal to the curve

· The equation of the tangent and normal to the curve (simple problems only)

3.3

Marginal Cost

and Marginal Revenue using derivatives

· Define marginal cost and marginal revenue

· Find marginal cost and marginal revenue

· Examples related to marginal cost, marginal revenue, etc.

3.4

Increasing

/Decreasing

Functions

· Determine whether a function is increasing or decreasing

· Determine the conditions for a function to be increasing or

decreasing

· Simple problems related to increasing and decreasing behaviour of a function in the

given interval

3.5

Maxima and

Minima

· Determine critical points of the function

· Find the point(s) of local maxima and local minima and

corresponding local maximum

and local minimum values

· Find the absolute maximum and absolute minimum value of a function

· Solve applied problems

· A point x= c is called the critical

point of f if

f is defined at c and

f ′ (c) =

0 or f is not differentiable

at c

· To find local maxima and local minima by:

i) First Derivative Test

ii) Second Derivative Test

· Contextualized real life problems

Integration and its Applications

3.5

Integration

· Understand and determine indefinite integrals of simple

functions as anti-derivative

· Integration as a reverse process of differentiation

· Vocabulary and Notations related to Integration

3.6

Indefinite

Integrals as family of

curves

· Evaluate indefinite integrals of simple algebraic functions by

method of:

i) substitution

ii) partial fraction iii) by parts

· Simple integrals based on each method (non-

trigonometric function)

3.7

Definite

Integrals as area under the

curve

● Define definite integral as area under the curve

● Understand fundamental theorem of Integral calculus and

apply it to evaluate the definite

integral

● Apply properties of definite integrals to solve the problems

● Evaluation of definite integrals using properties

3.9

Application of

Integration

● Identify the region representing

C.S. and P.S. graphically

● Apply the definite integral to find consumer surplus-producer surplus

Problems based on finding

● Total cost when Marginal Cost is given

● Total Revenue when Marginal

Revenue is given

● Equilibrium price and equilibrium quantity and hence consumer and producer surplus

Differential Equations and Modeling

3.10

Differential

Equations

● Recognize a differential equation

● Find the order and degree of a differential equation

● Definition, order, degree and examples

3.11

Formulating and Solving Differential

Equations

● Formulate differential equation

● Verify the solution of differential

equation

● Solve simple differential equation

● Formation of differential equation by eliminating arbitrary constants

● Solution of simple differential equations (direct integration only)

3.12

Application of

Differential

Equations

● Define Growth and Decay

Model

● Apply the differential equations to solve Growth and Decay Models

● Growth and Decay Model in Biological sciences, Economics and business, etc.

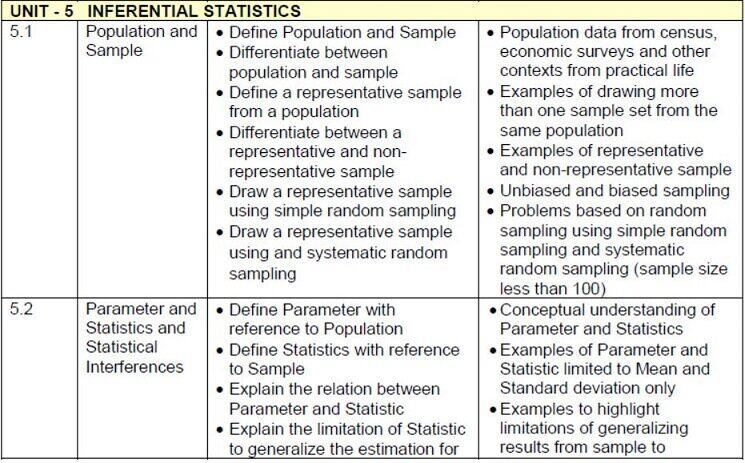
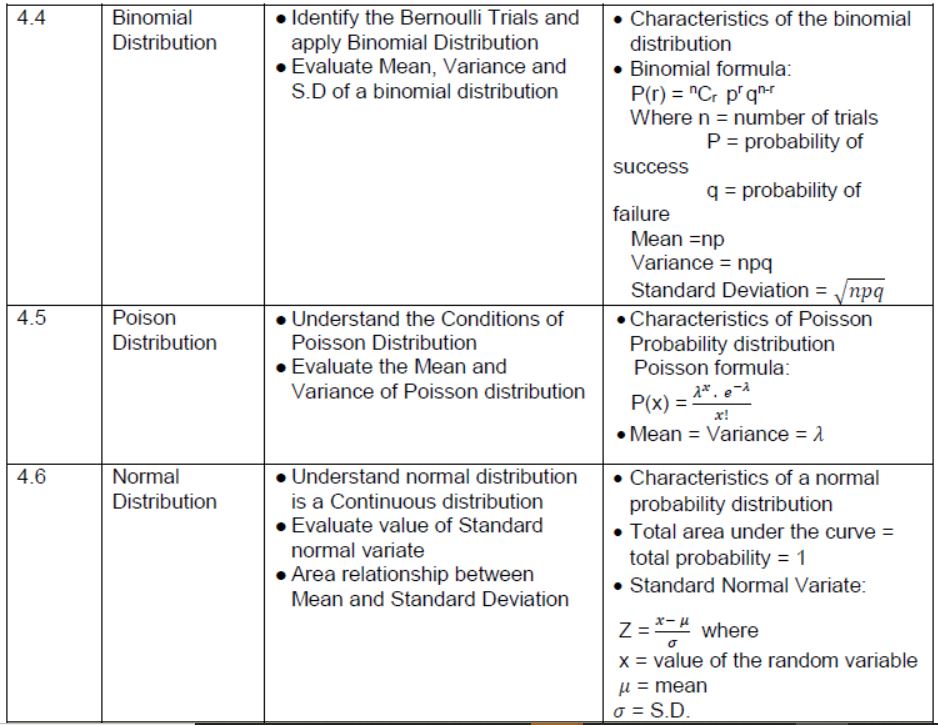
UNIT- 4 PROBABILITY DISTRIBUTIONS

4.1

Probability

Distribution

● Understand the concept of Random Variables and its Probability Distributions

● Find probability distribution of discrete random variable

· Definition and example of discrete and continuous random variable and their distribution

4.2

Mathematical

Expectation

● Apply arithmetic mean of frequency distribution to find the expected value of a random

variable

· The expected value of discrete random variable as summation

of product of discrete random

variable by the probability of its occurrence.

4.3

Variance

● Calculate the Variance and S.D. of a random variable

· Questions based on variance and standard deviation

Practical: Use of spreadsheet

Graphs of an exponential function, demand and supply functions on Excel and study the nature of function at various points, maxima/minima

Matrix operations using Excel

Suggested practical using the spreadsheet

i) Plot the graphs of functions on excel and study the graph to find out the point of maxima/minima

ii) Probability and dice roll simulation

iii) Matrix multiplication and the inverse of a matrix iv) Stock Market data sheet on excel

v) Collect the data on weather, price, inflation, and pollution analyze the data and make meaningful inferences

vi) Collect data from newspapers on traffic, sports activities and market trends and use excel to study future trends

List of Suggested projects (Class XI /XII)

i) Use of prime numbers in coding and decoding of messages

ii) Prime numbers and divisibility rules

iii) Logarithms for financial calculations such as interest, present value, future value, profit/loss etc. with large values)

iv) The cardinality of a set and orders of infinity

v) Comparing sets of Natural numbers, rational numbers, real numbers and others vi) Use of Venn diagram in solving practical problems

vii) Fibonacci sequence: Its' history and presence in nature

viii) Testing the validity of mathematical statements and framing truth tables ix) Investigating Graphs of functions for their properties

x) Visit the census site of India http://www.censusindia.gov.in/Census_Data_2001/Census_Data_Online/Languag e/State ment3.htm Depict the information given there in a pictorial form

xi) Prepare a questionnaire to collect information about money spent by your friends in a month on activities like travelling, movies, recharging of the mobiles, etc. and draw interesting conclusions

xii) Check out the local newspaper and cut out examples of information depicted by graphs. Draw your own conclusions from the graph and compare it with the analysis given in the report

xiii) Analysis of population migration data – positive and negative influence on urbanization

xiv) Each day the newspaper tells us about the maximum temperature, minimum temperature, and humidity. Collect the data for a period of 30 days and represent it graphically. Compare it with the data available for the same time period for the previous year

xv) Analysis of career graph of a cricketer (batting average for a batsman and bowling average for a bowler). Conclude the best year of his career. It may be extended for other players also – tennis, badminton, athlete

xvi) Vehicle registration data – correlating with pollution and the number of accidents

xvii) Visit a village near Delhi and collect data of various crops over the past few years from the farmers. Also, collect data about temperature variation and rain over the period for a particular crop. Try to find the effect of temperature and rain variations on various crops

xviii) Choose any week of your ongoing semester. Collect data for the past 10 – 15 years for the amount of rainfall received in Delhi during that week. Predict the amount of rainfall for the current year

xix) Weather prediction (prediction of monsoon from past data)

xx) Visit Kirana shops near your home and collect the data regarding the sales of certain commodities over a month. Try to figure out the stock of a particular commodity which should be in the store in order to maximize the profit

xxi) Stock price movement

xxii) Risk assessments by insurance firms from data xxiii) Predicting stock market crash

xxiv) Predicting the outcome of an election – exit polls

xxv) Predicting mortality of infants

Assessment Plan

1. Overall Assessment of the course is out of 100 marks.

2. The assessment plan consists of an External Exam and Internal Assessment.

3. External Exam will be of 03 hours duration Pen/ Paper Test consisting of 80 marks.

4. The weightage of the Internal Assessment is 20 marks. Internal Assessment can be a combination of activities spread throughout the semester/ academic year. Internal Assessment activities include projects and excel based practical. Teachers can choose activities from the suggested list of practicals or they can plan activities of a similar nature. For data-based practical, teachers are encouraged to use data from local sources to make it more relevant for students.
5.Weightage for each area of internal assessment may be as under:

Sl. No.	Area and Weightage	Assessment Area	Marks allocated
1	Project work (10 marks)	Project work and record	5
1	Project work (10 marks)	Year-end Presentation/ Viva of the Project	5
2	Practical work (10 marks)	Performance of practical and record	5
2	Practical work (10 marks)	Year-end test of any one practical	5
Total			20