CBSE Class 12 Maths Exam 2025 Important Questions: The Central Board of Secondary Education is the largest and one of the most famed school boards in India, and lakhs of students are currently enrolled in it. The CBSE conducts the Class 12 board exams annually. Maths is essential for non-medical science and commerce aspirants and is also required in subjects like physics, statistics and accounts. CBSE Class 12 Maths requires extensive practice, especially important topics like Calculus and Algebra. There will be five sections in the 2025 CBSE Class 12 Maths exam, and the last section E will comprise two case study-based questions of 4 marks. These questions are quite important from the exam point of view, and you can check and practice the solved versions here.
Check: CBSE Class 12 Maths Half Yearly Sample Paper 2025
CBSE Class 12 Maths Unit Wise Marks Distribution 2025
Check the unit-wise weightage here. Follow this for your exam preparation. Pick high weightage units first.
| No. | Units | Marks |
| I | Relations and Functions | 08 |
| II | Algebra | 10 |
| III | Calculus | 35 |
| IV | Vectors and Three - Dimensional Geometry | 14 |
| V | Linear Programming | 05 |
| VI | Probability | 08 |
|
| Total | 80 |
|
| Internal Assessment | 20 |
Related:
CBSE Class 12 Maths Case Study Questions 2025
Question 1: Ramesh is elder brother of Suresh. Ramesh wants to help his younger brother Suresh to solve the following problems of integrals. Write the suitable substitution by which Ramesh can help him.
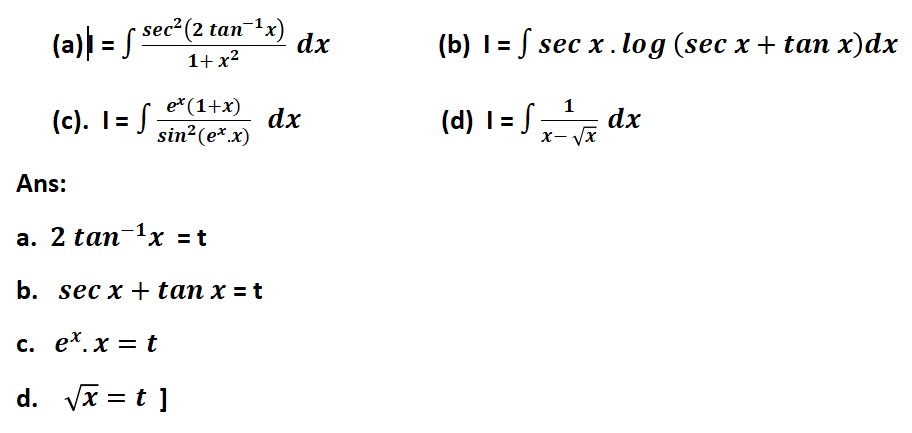
Question 2: Mr Shashi, who is an architect, designs a building for a small company. The design of window on the ground floor is proposed to be different than other floors. The window is in the shape of a rectangle which is surmounted by a semi-circular opening. This window is having a perimeter of 10 m as shown below :
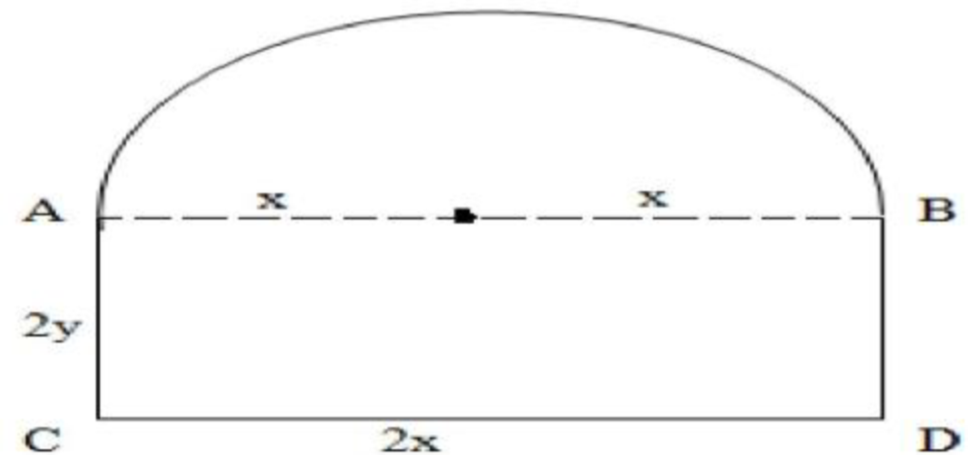
Based on the above information answer the following :
(i) If 2x and 2y represents the length and breadth of the rectangular portion of the windows, then the relation between the variables is:
(ii) The combined area (A) of the rectangular region and semi-circular region of the window expressed as a function of x is:
(iii) The maximum value of area A, of the whole window is
OR
The owner of this small company is interested in maximizing the area of the whole window so that maximum light input is possible.
For this to happen, the length of rectangular portion of the window should be
Answer:
(i) 4y = 10 - (2 + π)x
(ii) A = 10x - (2 + 12π)x2
(iii) 50/4 + π
OR
20/4 + π
Question 3: Read the following and answer the questions given below
The front gate of a building is in the shape of a trapezium as shown below. Its three sides other than base are of 10 m each. The height of the gate is h meter. On the basis of below figure, answer the following questions:
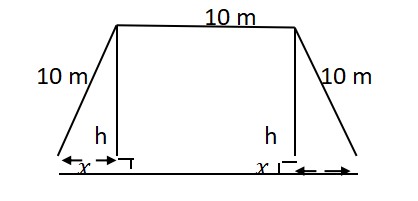
(i) Write the Area (A) of the gate in terms of .
(ii) Write the value of when Area (A) is maximum.
(iii) Write the value of h when Area (A) is maximum .
OR
Write the Maximum value of Area (A) .
Answer:
(i) (10 + x)√100 - x2
(ii) 5m
(iii) 5√3m OR 75√3/m.m2
Question 4: Read the following and answer the questions given below
Given three identical boxes 1st, 2nd and 3rd each containing two coins. In 1st box both coins are gold coins, in 2nd box both are silver coins and in 3rd box there is one gold and one silver coin. A person chooses a box at random and takes out a coin.
On the basis of above information, answer the following questions:
(i) What is the probability of choosing 1st box ?
(ii) What is the probability of getting gold coin from 3rd box ?
(iii) What is the total probability of drawing gold coin ?
OR
If drawn coin is of gold the probability that other coin in the box is also of gold?
Answer:
(i) 1/3
(ii) 1/2
(iii) 1/2 Or 2/3
Question 5: Read the following and answer the questions given below
Sand is pouring from a pipe at the rate of 12 cm3/ second the falling sand forms a cone on the ground in such a way that the height of the cone is always 1/6th of the radius of the base. Based on above information answer the following:
(i) Write the expression for volume in terms of height only.
(ii) What is the rate of Change of height, when height is 4 cm?
Answer:
i) 12πh3
(ii) 1/48 cm/s
Question 6: There are two antiaircraft guns, named as A and B. The probabilities that the shell fired from them hits an airplane are 0.3 and 0.2 respectively. Both of them fired one shell at an airplane at the same time.
(i) What is the probability that the shell fired from exactly one of them hit the plane?
(ii) If it is known that the shell fired from exactly one of them hit the plane, then what is the probability that it was fired from B?
Answer:

7. Ramesh, the owner of a sweet selling shop, purchased some rectangular card board sheets of dimension 25 by 40 cm cm to make container packets without top. Let x cm be the length of the side of the square to be cut out from each corner to give that sheet the shape of the container by folding up the flaps. Based on the above information answer the following questions.
Answer:
8. Arka bought two cages of birds: Cage-I contains 5 parrots and 1 owl and Cage –II contains 6 parrots. One day Arka forgot to lock both cages and two birds flew from Cage-I to Cage-II (simultaneously). Then two birds flew back from cage-II to cage-I(simultaneously). Assume that all the birds have equal chances of flying. On the basis of the above information, answer the following questions:-
(i) When two birds flew from Cage-I to Cage-II and two birds flew back from Cage-II to Cage-I then find the probability that the owl is still in Cage-I.
(ii) When two birds flew from Cage-I to Cage-II and two birds flew back from Cage-II to Cage-I, the owl is still seen in Cage-I, what is the probability that one parrot and the owl flew from Cage-I to Cage-II?
Answer:
Why Are Case-Based Questions are Important for Your Exam?
These questions are not just for a quick check of your knowledge; they are a significant part of your total score.
High Marks: Section E questions typically carry 4 marks each, and there are multiple such questions in the paper. Performing well here can significantly boost your overall score.
Application over Memorization: They test your conceptual understanding and problem-solving skills rather than just your ability to recall formulas. This is a chance to show that you truly understand the subject.
Confidence Booster: Once you get the hang of them, these questions can be some of the easiest to score on because the context and most of the data are already given to you.
Also Read:
Other Important Study Resources for CBSE Class 12 Exams
Comments
All Comments (0)
Join the conversation