CBSE Class 12 Mathematics Chapter 4 Determinants Revision Notes: With the 2024 board exams around the corner, the time to put down the books and begin revising the topics is here. Mathematics is a subject that requires consistent practice and thorough revision. In the last stage of the session year, it’s advised to students to revise what they know instead of picking up new topics to study.
The CBSE Class 12 exams are set to begin from February 15, 2024, and the mathematics paper will be on March 9. The fourth chapter in the Class 12 math books is Determinants. It’s an important chapter in the course and holds a substantial weightage in the final exam. You can check out the CBSE Class 12 Chapter 4 Determinants revision notes here, along with supporting study material like mind maps and multiple choice questions.
CBSE Class 12 Maths Chapter 4 Determinants Revision Notes
Basic Definitions and Summary:
A determinant is a numerical scalar value associated with a square matrix.
If A = [aij], then determinant = det(A) or |A|
Determinant of a matrix A = [a11]1×1 is given by |a11| = a11
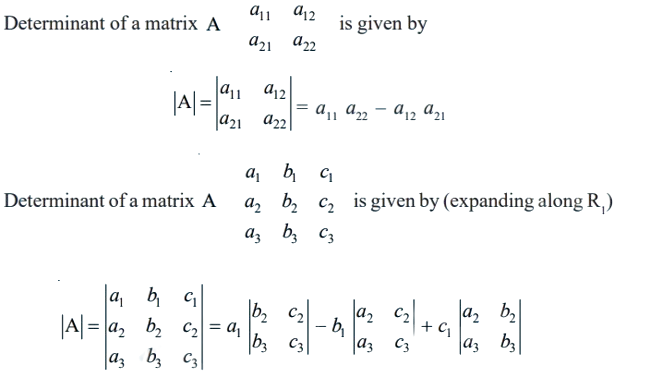
For any square matrix A, the |A| satisfy the following properties.
Area of a triangle with vertices (x1 , y1 ), (x2 , y2 ) and (x3 , y3 ) is given by
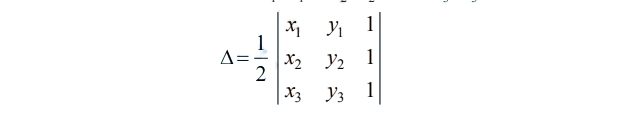
Minor of an element aij of the determinant of matrix A is the determinant obtained by deleting ith row and jth column and denoted by Mij.
Co-factor of aij of given by Aij = (– 1)i+ j Mij
The value of determinant of a matrix A is obtained by the sum of product of elements of a row (or a column) with corresponding co-factors. For example, A = a11 A11 + a12 A12 + a13 A13.
If elements of one row (or column) are multiplied with co-factors of elements of any other row (or column), then their sum is zero. For example, a11 A21 + a12 A22 + a13 A23 = 0
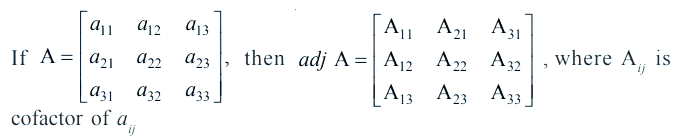
A (adj A) = (adj A) A = |A| I, where A is the square matrix of order n.
A square matrix A is said to be singular or non-singular according as |A| = 0 or |A| ≠ 0.
If AB = BA = I, where B is a square matrix, then B is called the inverse of A.
Also, A–1 = B or B–1 = A and hence (A–1)–1 = A.
A square matrix A has an inverse if and only if A is non-singular.
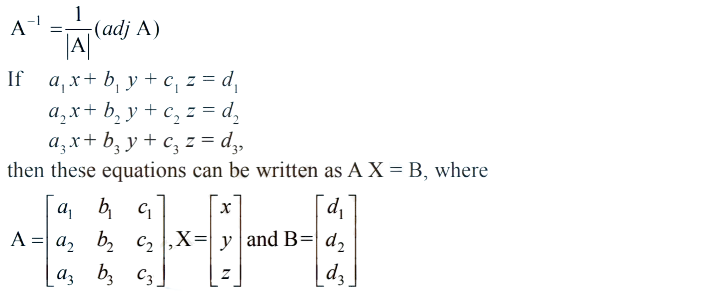
The unique solution of equation AX = B is given by X = A–1 B, where A 0 ≠.
A system of equations is consistent or inconsistent according as its solution exists or not.
For a square matrix A in matrix equation AX = B.
(i) |A| ≠ 0, there exists a unique solution
(ii) |A| = 0 and (adj A) B ≠ 0, then there exists no solution.
(iii) |A| = 0 and (adj A) B = 0, then system may or may not be consistent.
CBSE Class 12 Maths Chapter 4 Determinants Revision Notes PDF |
Comments
All Comments (0)
Join the conversation