CBSE Class 12 Maths Chapter 5 Continuity and Differentiability Revision Notes Download PDF

CBSE Class 12 Mathematics Chapter 5 Continuity and Differentiability Revision Notes: With the 2024 board exams around the corner, the time to put down the books and begin revising the concepts has arrived. Mathematics requires consistent practice and thorough revision. In the final months of the session year, students are advised to revise what they know instead of learning new concepts.

The CBSE Class 12 exams are set to commence from February 15, 2024, and the mathematics paper will be held on March 9. The fifth chapter in the Class 12 math books is Continuity and Differentiability. It’s a key chapter in the curriculum and holds considerable importance in the final exam. You can check out the CBSE Class 12 Chapter 5 Continuity and Differentiability revision notes here, along with supporting study material like mind maps and multiple choice questions.

CBSE Class 12 Maths Chapter 5 Continuity and Differentiability Revision Notes

Basic Definitions and Summary:

A real-valued function is continuous at a point in its domain if the limit of the function at that point equals the value of the function at that point. A function is continuous if it is continuous on the whole of its domain.

The sum, difference, product and quotient of continuous functions are continuous.

i.e., if f and g are continuous functions, then

(f ± g) (x) = f(x) ± g(x) is continuous.

(f . g) (x) = f(x) . g(x) is continuous

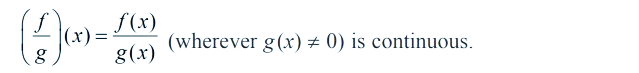
Algebra of Continuous Functions

Theorem 1: Suppose f and g be two real functions continuous at a real number c. Then

(1) f + g is continuous at x = c.

(2) f – g is continuous at x = c.

(3) f . g is continuous at x = c.

(4) (f/g) is continuous at x = c, (provided g (c) ≠ 0).

Proof: We are investigating the continuity of (f + g) at x = c. Clearly, it is defined at x = c. We have

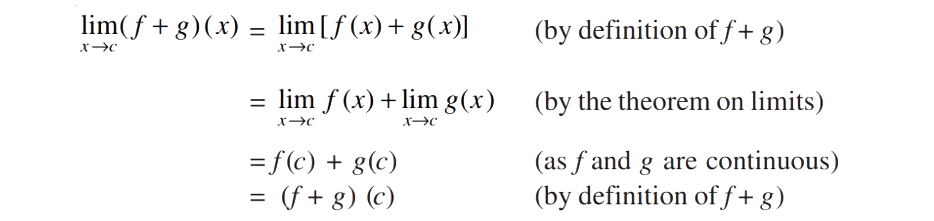
Hence, f + g is continuous at x = c. Proofs for the remaining parts are similar and left as an exercise to the reader.

Every differentiable function is continuous, but the converse is not true.

The chain rule is a rule to differentiate composites of functions. If f = v o u, t = u (x) and if both dt/dx and dv/dt exist then

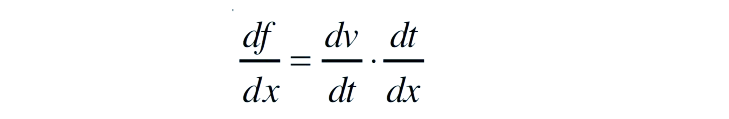
Following are some of the standard derivatives (in appropriate domains):

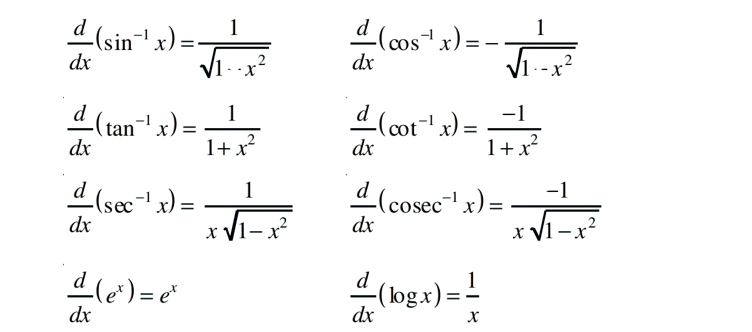
Theorem 3: If a function f is differentiable at a point c, then it is also continuous at that point.

Proof: Since f is differentiable at c, we have

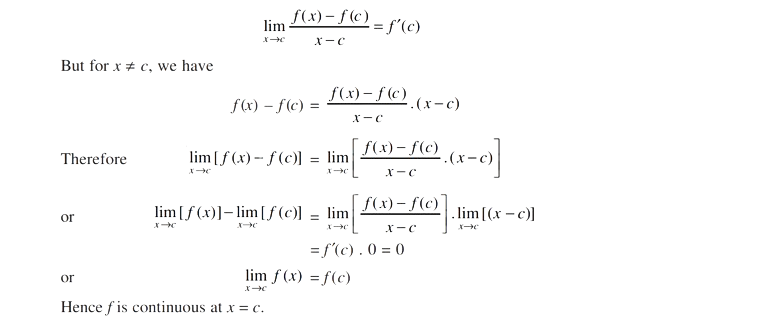
Logarithmic differentiation is a powerful technique to differentiate functions of the form f(x) = [u (x)]v (x). Here both f(x) and u(x) need to be positive for this technique to make sense.

Recommended:

Class 12 Maths Chapter 5 Continuity and Differentiability NCERT Solutions

CBSE Class 12 Maths Chapter 5 Continuity and Differentiability MCQs

CBSE Class 12 Chapter 5 Continuity and Differentiability Mind Map, Download PDF

CBSE Class 12 Maths Chapter 5 Continuity and Differentiability Formulas