Electrostatic Potential and Capacitance Class 12 Notes: CBSE 12th Physics Chapter 2, Download PDF

2.2 ELECTROSTATIC POTENTIAL

• The electrostatic potential at any point in an electric field is equal to the amount of work done per unit positive test charge or in bringing the unit positive test charge from infinite to that point, against the electrostatic force without acceleration. electrostatic potential V = [ work done (W) / Charge (Q)]
• Electrostatic force is a conservative force. Work done by an external force (equal and opposite to the electrostatic force) in bringing a charge q from a point R to a point P is q(VP–VR), which is the difference in potential energy of charge q between the final and initial points. 

• Potential at a point is the work done per unit charge (by an external agency) in bringing a charge from infinity to that point. Potential at a point is arbitrary to within an additive constant, since it is the potential difference between two points which is physically significant. If potential at infinity is chosen to be zero; potential at a point with position vector r due to a point charge Q placed at the origin is given is given by 
  

2.3 POTENTIAL DUE TO A POINT CHARGE

2.4 POTENTIAL DUE TO AN ELECTRIC DIPOLE

The electrostatic potential at a point with position vector r due to a point dipole of dipole moment p placed at the origin is

The result is true also for a dipole (with charges –q and q separated by 2a) for r >> a.

2.5 POTENTIAL DUE TO A SYSTEM OF CHARGES

For a charge configuration q1, q2, ..., qn with position vectors r1, r2, ... rn, the potential at a point P is given by the superposition principle where r1P is the distance between q1 and P, as and so on.

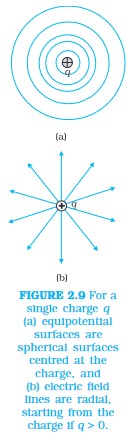
2.6 EQUIPOTENTIAL SURFACES

An equipotential surface is a surface over which potential has a constant value.

For a point charge, concentric spheres centred at a location of the charge are equipotential surfaces.

The electric field E at a point is perpendicular to the equipotential surface through the point.

E is in the direction of the steepest decrease of potential.

For a single charge q, the potential is given

by 

2.6.1 Relation between field and potential

The relation between electric field (E) and electric potential (V) is given by the following equation:

E = - dV/dx

Where:

- E is the electric field strength at a particular point in space.

- V is the electric potential at that point.

- dx is the infinitesimal displacement along the x-direction.

It means that the electric field points in the direction of the steepest decrease in electric potential. 

Electric potential is a scalar quantity, whereas the electric field is a vector quantity. 

The direction of the electric field is from higher potential to lower potential. 

Therefore, when moving in the direction of the electric field, the electric potential decreases. Conversely, if one moves against the electric field, the electric potential increases.

2.7 POTENTIAL ENERGY OF A SYSTEM OF CHARGES

For charges Q1 an Q2

For a system of 3 charges:

2.8 POTENTIAL ENERGY IN AN EXTERNAL FIELD

2.8.1 Potential energy of a single charge

Work done in bringing a charge q from infinity to the point P in the external field is qV.

This work is stored in the form of potential energy of q. If the point P has position vector r relative to some origin, we can write:

Potential energy of q at r in an external field = qV (r), where V(r) is the external potential at the point r.

2.8.2 Potential energy of a system of two charges in an external field

Potential energy of a system of two charges q1 and q2 located at r1and r2

2.8.3 Potential energy of a dipole in an external field

The potential energy of a dipole moment p in a uniform electric field E is –p.E.

2.9 ELECTROSTATICS OF CONDUCTORS

• Inside a conductor, electrostatic field is zero
• At the surface of a charged conductor, electrostatic field must be normal to the surface at every point
• The interior of a conductor can have no excess charge in the static situation
• Electrostatic potential is constant throughout the volume of the conductor and has the same value (as inside) on its surface
• Electric field at the surface of a charged conductor is
  
• Electrostatic shielding: The process which involves the making of a region free from any electric field is known as electrostatic shielding.

2.10 DIELECTRICS AND POLARISATION

Dielectrics are non-conducting substances. 

Difference in behaviour of a conductor and a dielectric in an external electric field:

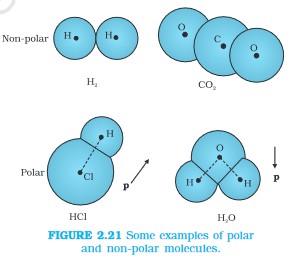
Polar molecules: centres of positive and negative charges are separated and have permanent dipole moments. 

Non-polar molecules:Centres of positive andnegative charges coincide and have no permanent dipole moment.

A uniformly polarised dielectric amounts to induced surface charge density, but no volume charge density.

2.11 CAPACITORS AND CAPACITANCE

• A capacitor is a system of two conductors separated by an insulator.
• The total charge of the capacitor is zero.
• The conductors have charges, say Q1 and Q2, and potentials V1 and V2.
• Capacitance of the capacitor = C = Q / V
• The capacitance C depends only on the geometrical configuration (shape, size, separation) of the system of two conductors.
• The unit of capacitance is farad: 1 F = 1 C V –1.

2.12 THE PARALLEL PLATE CAPACITOR

A parallel plate capacitor consists of two large plane parallel conducting plates separated by a small distance.

For a parallel plate capacitor (with vacuum between the plates),

where A is the area of each plate and d the separation between them.

2.13 EFFECT OF DIELECTRIC ON CAPACITANCE

If the medium between the plates of a capacitor is filled with an insulating substance (dielectric), the electric field due to the charged plates induces a net dipole moment in the dielectric. This effect, called polarisation, gives rise to a field in the opposite direction. The net electric field inside the dielectric and hence the potential difference between the plates is

thus reduced. Consequently, the capacitance C increases from its value C0 when there is no medium (vacuum),

C = KC0

where K is the dielectric constant of the insulating substance.

2.14 COMBINATION OF CAPACITORS

2.14.1 Capacitors in series and 2.14.2 Capacitors in parallel

2.15 ENERGY STORED IN A CAPACITOR

Download CBSE Class 12 Physics Ch 2 Electrostatic Potential and Capacitance Notes PDF