Kinematics Equation: Definition, Explanation, Formulas And Applications

Kinematics Equation: The branch of physics that defines motion concerning space and time, ignoring the cause of that motion, is known as Kinematics. Kinematics equations are a set of formulas used in physics to describe the motion of an object in a straight line. There are four key variables of motion. 

• Acceleration (a)- the rate of change of an object’s velocity over time. 
• Displacement (s)- the total distance and the direction the object travels. 
• Final Velocity (v)- the object’s velocity at the end of the time interval. 
• Initial Velocity (u)- the object’s velocity at the beginning of the time interval. 

There are three basic kinematic equations: 

• V= u+at = This equation relates to an object’s initial velocity, final velocity, acceleration and time. It tells how much the object’s velocity changes due to constant acceleration over a specific time. 
• s= ut+½ a(t^2)= This equation relates the object’s displacement, initial velocity, acceleration and time. It is the total distance travelled considering both the initial velocity and the effect of acceleration over time. 
• v^2 = u^2 + 2as: This equation relates the object’s final velocity squared, and initial velocity squared along with acceleration and displacement. 

Note: Kinematic Equations are only applicable at a constant acceleration or a constant speed, and we cannot use them if either of the two is changing. 

How do you select and use a kinematic equation? 

We chose the kinematic equation that includes both the unknown variable we are looking for and the three of the kinematic variables we already know. This way, we can easily solve the unknown variable for which we need to find out the solution. 

Derivation Of First Equation

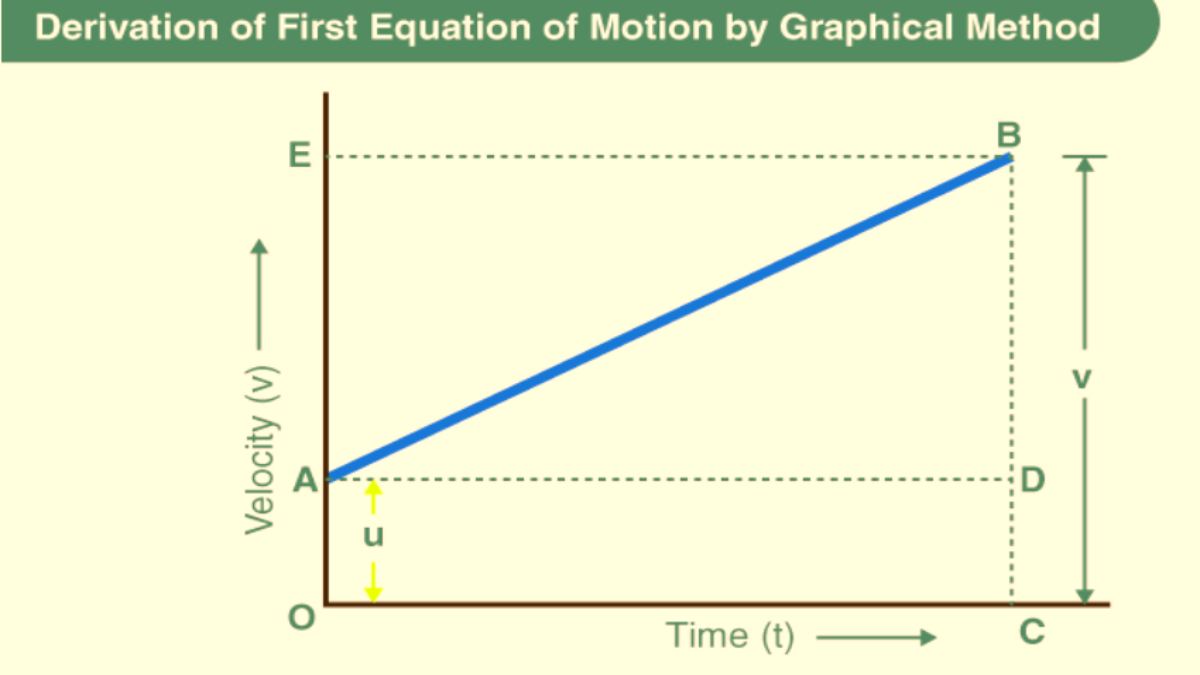
The first equation can be derived using a velocity-time graph for a moving object with an initial velocity of u, final velocity of v and acceleration of a. 

• The velocity of the body changes from A to B in the time t at a uniform rate. 
• BC is the final velocity and OC is the total time t. 
• A perpendicular can be drawn from B to OC a parallel line is drawn from A to D, and another perpendicular is drawn from B to OE. 

The initial velocity= OA

Final Velocity= BC 

From the graph, we can get the following: 

BC= BD+DC

So, V= BD+OA, 

Now V= BD+ u as OA=u

Now, the slope of the velocity-time graph is equal to acceleration a. So, 

a= slope of line AB, a= BD/AD

AD = AC = t, so the equation becomes 

v= u + at

Derivation Of Second Equation

Distance travelled (s)= Area Of Figure OABC = Area of rectangle OADC + Area of triangle ABD

s= (½ x AD x BD) + (OA x OC) 

s= ½ x t x at + ut

s= ut+ ½ at^2

Derivation Of Third Equation

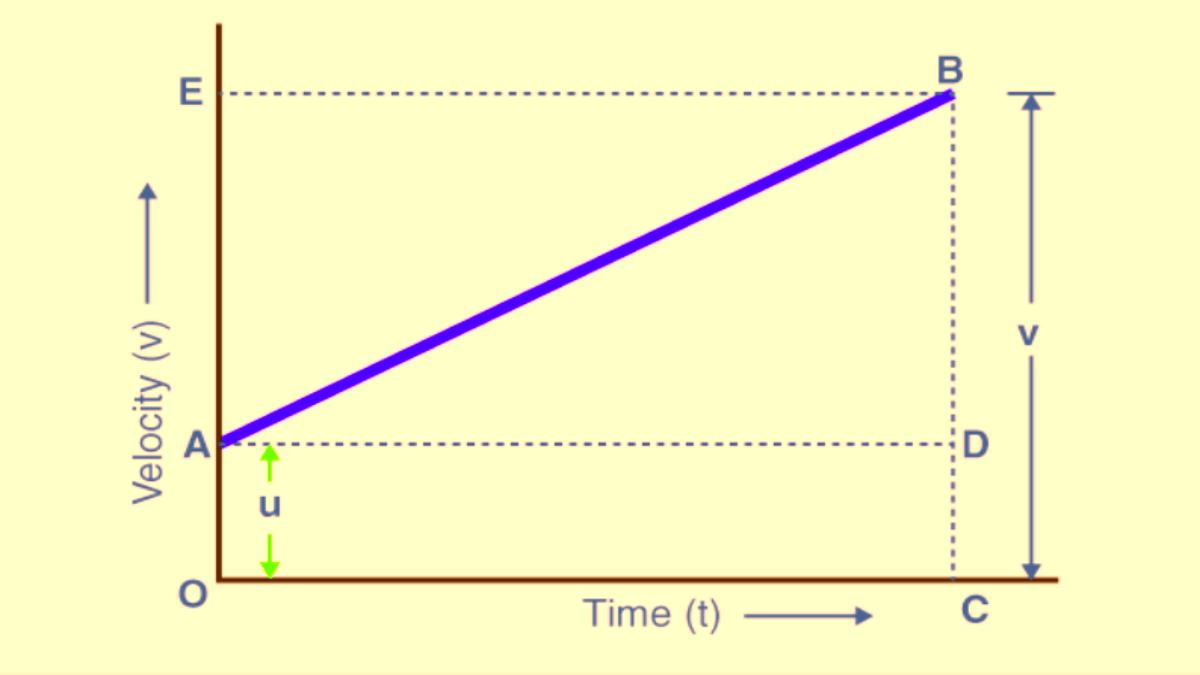
The area of trapezium OABC can give the total distance travelled which is = s. 

s = ½ × (Sum of Parallel Sides) × Height

s = 1/2 x (OA + CB) x OC

Since, OA = u, CB = v, and OC = t

The above equation now becomes, 

s = 1/2 x (u+v) x t

Rearranging the equation, you can get

s = ½ x ((u+v) × (v-u))/a

s = ½ x (v+u) × (v-u)/a

s = (v2-u2)/2a

Applications Of Kinematics Equation

The Kinematics equation can be used to explain the concept of projectile motion and the robot arm movement. 

We hope that with the help of this article, students can understand the basic concept of kinematic equations and make the learning process with the help of these notes. 

We are also providing video lessons for students available on the Jagran Josh portal. Tap on the link below to listen to the video lessons by Subject Matter Experts. 

Video Lessons Link

• CBSE Class 12 Science Video Lessons By Subject Matter Experts
• CBSE Class 11 Science Video Lessons By Subject Matter Experts

Other Related Links

• West Bengal Board Class 11 Anthropology Syllabus 2024-25: Download The Syllabus PDF For Free!

• West Bengal Board Class 11 Health And Physical Education Syllabus 2024-25: Download Syllabus PDF For Free!