NCERT Solutions for Class 10 Maths Chapter 3, Pair of Linear Equations in Two Variables: Practicing NCERT questions will help students build their understanding and problem-solving skills. These questions are also important from the exam point of view as many times the questions have been asked directly and indirectly in the CBSE Board Exams. In this article, we have provided the NCERT solutions for Class 10 Math Chapter 3 - Pair of Linear Equations in Two Variables
You will get the step-by-step solutions to the questions given in the Chapter 3 Pair of Linear Equations in Two Variables. This helps students to understand the application of concepts and how to approach different types of questions in the examination. All the solutions have been collated in PDF format which students can easily download for free and start practicing for their board exam and score well.
NCERT Solutions of Pair of Linear Equations in Two Variables are as follows:
Find the complete solutions of all the exercise questions step-by-step, to get all the solutions in the PDF format click the link below and download the complete solutions.
Exercise 3.1
1. Form the pair of linear equations in the following problems, and find their solutions graphically.
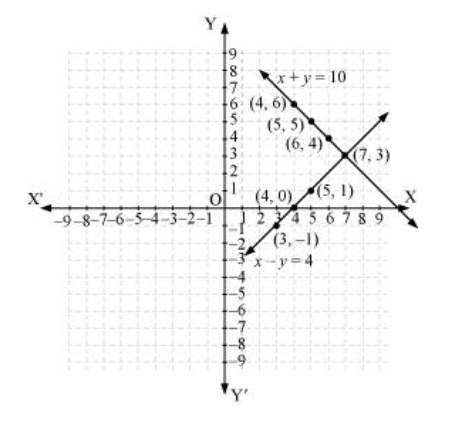
(i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
Let the number of girls = x
The number of boys = y
As per the question,
x + y = 10
x - y = 4
Now,
x + y =10
| X | 5 | 4 | 6 |
| Y | 5 | 6 | 4 |
x - y = 4
| X | 5 | 4 | 3 |
| Y | 1 | 0 | -1 |
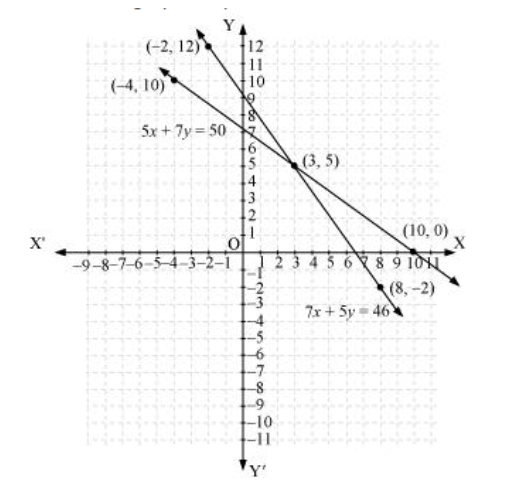
(ii) 5 pencils and 7 pens together cost ` 50, whereas 7 pencils and 5 pens together cost ` 46. Find the cost of one pencil and that of one pen.
Let the cost of 1 pencil = Rs x
The cost of 1 pen = Rs y.
As per the question,
5x 7 y 50
7x 5 y 46
Now,
5x + 7 y = 50
| X | 3 | 10 | -4 |
| Y | 5 | 0 | 10 |
7x + 5y = 46
| X | 8 | 3 | -2 |
| Y | -2 | 5 | 12 |
2. On comparing the ratios a1/a2, b1/b2 and c1/c2, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident:
(i) 5x – 4y + 8 = 0
7x + 6y – 9 = 0
5x - 4 y + 8 = 0
7x + 6 y - 9 = 0
| a1 =5, | b1 = -4, | c1 = 8 |
| a2 = 7, | b2 = 6, | c2 = -9 |
a1/a2 = b1/b2
Equations have a unique solution and pair of lines intersects at exactly one point.
(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
9x + 3y +12 = 0
18x + 6 y + 24 = 0
| a1 =9, | b1 = 3, | c1 = 12 |
| a2 = 18, | b2 = 6, | c2 = 24 |
a1/a2 = b1/b2= c1/c2 (Infinite solution)
(iii) 6x – 3y + 10 = 0
2x – y + 9 = 0
6x – 3y + 10 = 0
2x – y + 9 = 0
| a1 =6, | b1 = -3, | c1 = 10 |
| a2 = 2, | b2 = -1, | c2 = 9 |
a1/a2 = b1/b2 = c1/c2 (No solution)
3. On comparing the ratios a1/a2, b1/b2 and c1/c2, find ut whether the following pair of linear equations are consistent, or inconsistent.
(i) 3x + 2y = 5 ; 2x – 3y = 7
Sol.
| a1 =3, | b1 = 2, | c1 = 5 |
| a2 = 2, | b2 = -3, | c2 = 7 |
a1/a2 ≠ b1/b2 (consistent)
(ii) 2x – 3y = 8 ; 4x – 6y = 9
Sol. a1/a2 = b1/b2 ≠ c1/c2 (inconsistent)
(iii) 3/2x + 5/3y = 7; 9x – 10y = 14
a1/a2 ≠ b1/b2 (consistent)
(iv) 5x – 3y = 11 ; – 10x + 6y = –22
a1/a2 = b1/b2 = c1/c2 (consistent)
(v) 4/3x + 2y = 8 ; 2x + 3y = 12
a1/a2 = b1/b2 = c1/c2 (consistent)
4. Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
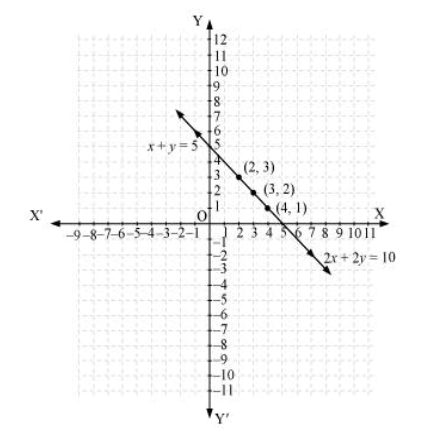
(i) x + y = 5, 2x + 2y = 10
x + y = 5, 2x + 2y = 10
Since, a1/a2 = b1/b2 = c1/c2
Solution is, x + y =5
| x | 4 | 3 | 2 |
| y | 1 | 2 | 3 |
2x + 2y = 10
| x | 4 | 3 | 2 |
| y | 1 | 2 | 3 |
(ii) x – y = 8, 3x – 3y = 16
Since, a1/a2 = b1/b2 ≠ c1/c2
Pair of equations is inconsistent
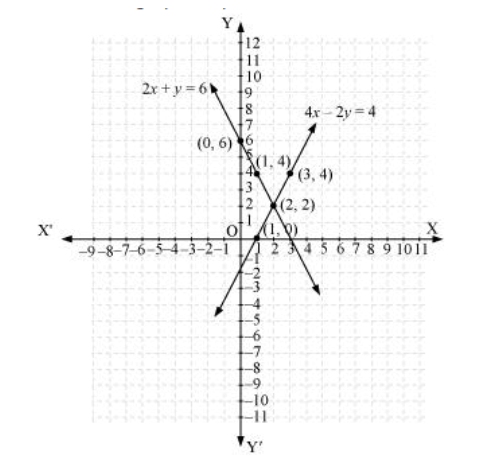
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
Since, a1/a2 ≠b1/b2
Solution is
2x + y - 6 = 0
| x | 0 | 1 | 2 |
| y | 6 | 4 | 2 |
4x - 2y -4 =0
| x | 1 | 2 | 3 |
| y | 0 | 2 | 4 |
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
Since, a1/a2 = b1/b2 ≠ c1/c2
Pair of equations is inconsistent
5. Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
Let the width of the garden = x
Length = y
According to the question,
y - x = 4
y + x = 36
Graphical representation:
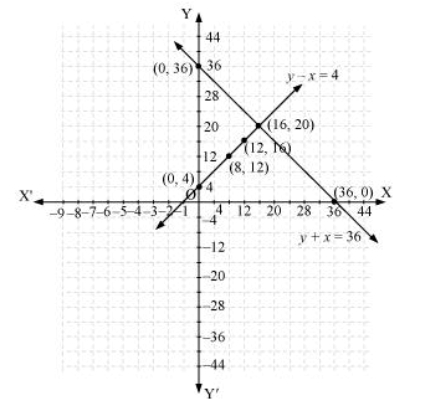
Hence, the length and width of the given garden is 20 m and 16 m respectively.
6. Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is:
(i) intersecting lines (ii) parallel lines
(iii) coincident lines
Intersecting lines:
a1/a2 ≠b1/b2
The second line will be:
2x + 4 y - 6 = 0
Parallel lines
a1/a2 = b1/b2 ≠ c1/c2
The second line will be:
4x + 6 y - 8 = 0
Coincident lines
a1/a2 = b1/b2 = c1/c2
The second line will be:
6x + 9 y - 24 = 0
7. Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
x - y + 1 = 0
3x + 2 y -12 = 0
Solution tables are:
| x | 0 | 1 | 2 |
| y | 1 | 2 | 3 |
| x | 4 | 2 | 0 |
| y | 0 | 3 | 6 |
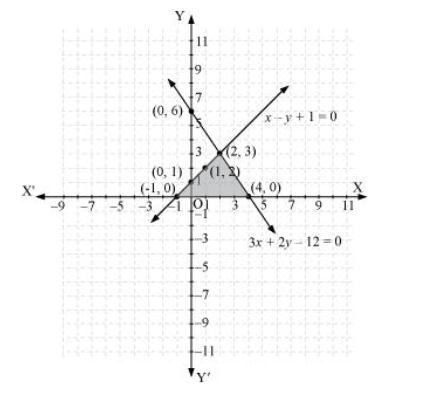
Therefore, the vertices of the triangle are (2, 3), (—1, 0), and (4, 0).
Exercise 3.2
1. Solve the following pair of linear equations by the substitution method.
(i) x + y = 14
x – y = 4
x + y = 14, x - y = 4
x + y = 14
x = 14 - y
Put value of x in equation 2
x - y = 4
14 - y - y = 4
-2 y = -10
y = 5
Now,
x =14- y
x = 14 - 5
x = 9
We have, x = 9, y = 5
(ii) s – t = 3
s/3+ t/2=6
s - t = 3
s = 3 + t
Put value of s in equation 2
s/3+ t/2=6
2s + 3t = 36
2(3 + t ) + 3t = 36
6 + 2t + 3t = 36
5t = 36 - 6
5t = 30
t = 6
Now,
s = 3 + t s = 3 + 6
s = 9
We have, s = 9,t = 6
(iii) 3x – y = 3
9x – 3y = 9
These equation has infinite possible solutions
solutions can be given by:
y = 3x - 3
(iv) 0.2x + 0.3y = 1.3
0.4x + 0.5y = 2.3
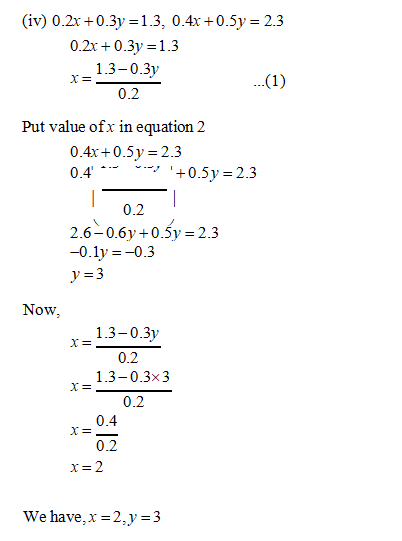
(v) √2x+√3y = 0
√3x - √8y = 0

(vi) 3x/2 - 5y/3 = -2
x/3 + y/2 = 13/6
3x/2 - 5y/3 = -2
3x/2 = -2 + 5y/3
3x/2 = -6+5y/3
x = -12 + 10y/9
put value of x in equation 2
x/3 + y/2 = 13/6
1/3 (-12 + 10y)/ (9), y/2-13/6
-12 + 10y/9 + 3y/2 = 13/2
12 + 10y/9 = 13/2 - 3y/2
-12+10y/9 = 13-3y/2
-24 + 20 y = 117 - 27 y
-24 -117 = -47 y
47 y = 141
y = 3
Now,
x= -12+10y/9
x= -12+10x3/9
x = 18/9
x = 2
We have, x = 2, y = 3
2. Solve 2x + 3y = 11 and 2x – 4y = – 24 and hence find the value of ‘m’ for which
y = mx + 3.
2x + 3y = 11
2x - 4 y = -24
2x + 3y = 11
x = 11-3y/2
Put value of x in equation 2 2x - 4 y = -24
x - 2 y = -12
11-3y/2 - 2y = -12
11- 3y - 4 y = -24
11- 7 y = -24
-7 y = -24 -11
7 y = 35
y = 5
Now,
x =11-3y/2
x = 11-3x5/2
x = -2
Now,
Y = mx + 3
5 = -2m + 3
-2m = 2
m = -1
3. Form the pair of linear equations for the following problems and find their solution by substitution method.
(i) The difference between two numbers is 26 and one number is three times the other. Find them.
Let the first number = x second number = y
As per the question,
y = 3x
y - x = 26
y = 3x
Put value of x in equation 2
y - x = 26 3x - x = 26
2x = 26
x = 13 ...(1)
y = 3x y = 39
The numbers are 13 and 39.
(ii) The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them.
Let the larger angle = x smaller angle = y
As per the question,
x + y = 180
x - y = 18
x + y = 180
x = 180 - y ...(1)
x - y = 18
180 - y - y = 18
-2 y = 18 -180
2 y = 162
y = 81
x = 180 - y x = 180 - 81
x = 99
Thus, angles are 99 and 81.
(iii) The coach of a cricket team buys 7 bats and 6 balls for ` 3800. Later, she buys 3 bats and 5 balls for ` 1750. Find the cost of each bat and each ball.
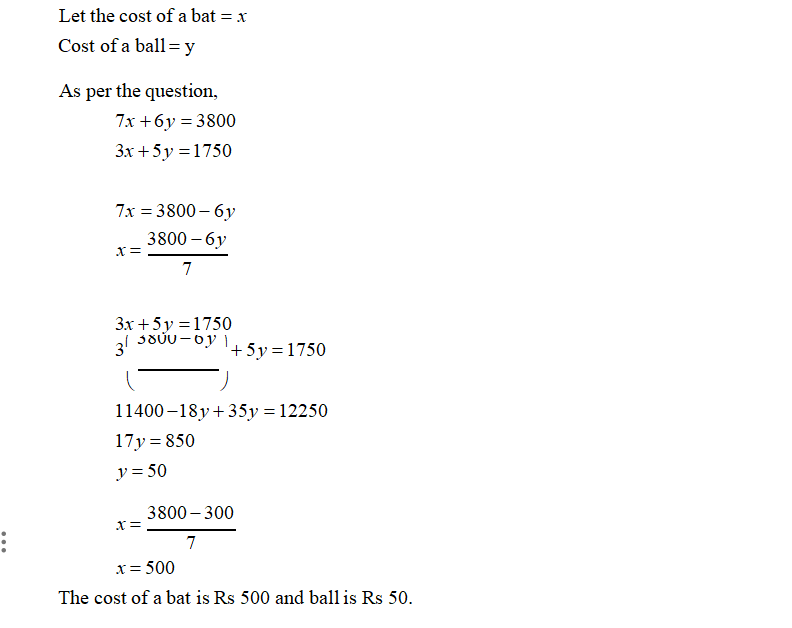
(iv) The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is ` 105 and for a journey of 15 km, the charge paid is ` 155. What are the fixed charges and the charge per km? How much does a person have to pay for traveling a distance of 25 km?
Let the fixed charges = Rs. x
per km charge = Rs y
As per the question,
x +10 y = 105
x +15 y = 155
x +10 y = 105
x = 105 -10 y
x +15 y = 155
105 -10 y +15 y = 155
5 y = 50
y = 10
x = 105 -100
x = 5
Hence, fixed charges = Rs. 5 per km charge = Rs. 10
charge for 25km = x + 25 y = 5 + 250 = Rs.255
(v) A fraction becomes 9/11, if 2 is added to both the numerator and the denominator. If 3 is added to both the numerator and the denominator it becomes 5/6. Find the fraction.
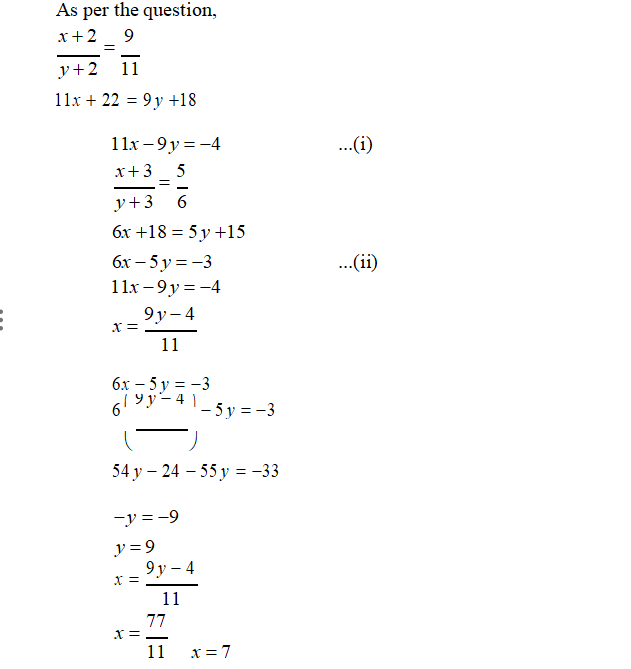
(vi) Five years hence, the age of Jacob will be three times that of his son. Five years ago, Jacob’s age was seven times that of his son. What are their present ages?
Let the age of jacob = x
age of his son = y
As per the question,
( x + 5) = 3( y + 5)
x - 3y = 10 ...(1)
( x - 5) = 7 ( y - 5)
x - 7 y = -30 ...(2)
x - 3y = 10
x = 10 + 3y
x - 7 y = -30
10 + 3y - 7 y = -30
-4 y = -40
y = 10
x = 10 + 3y
x = 40
Hence, present age of jacob is 40 years and of his son is 10 years.
Exercise 3.3
1. Solve the following pair of linear equations by the elimination method and the substitution method :
(i) x + y = 5 and 2x – 3y = 4
x + y = 5, 2x - 3y = 4 Elimination method
x + y = 5
2x - 3y = 4
Multiply the first equation by 2
2x + 2 y = 10
2x - 3y = 4
On subtracting the above equations, we got
5 y = 6
y = 6/5
x + y = 5
x = 5 - 6/5
x = 19/5
x = 19/5, y = 6/5
Substitution method
x + y = 5, 2x - 3y = 4
x = 5 - y
Put value of x in equation 2 2x - 3y = 4
2(5 - y ) - 3y = 4
10 - 2 y - 3y = 4
-5 y = -6
y = 6/5
x = 5 - y
x = 5 - 6/5
x = 19/5
x = 19/5, y = 6/5
(ii) 3x + 4y = 10 and 2x – 2y = 2
Elimination method
3x + 4 y = 10
2x - 2 y = 2
Multiply the second equation by 2 3x + 4 y = 10
4x - 4 y = 4
On adding aove equations 7x = 14
x = 2
2x - 2 y = 2
x - y = 1 2 - y = 1
y = 1
We have, x = 2, y =1 Substitution method
3x + 4 y = 10
2x - 2 y = 2
2x - 2 y = 2
x - y = 1
x = y + 1
Put value of x in equation 1 3x + 4 y = 10
3( y + 1) + 4 y = 10
3y + 3 + 4 y = 10
7 y = 7
y = 1
x = y +1
x = 2
We have, x = 2, y = 1
(iii) 3x – 5y – 4 = 0 and 9x = 2y + 7


(iv) x/2 + 2y/3 = -1 and x- y/3 = 3

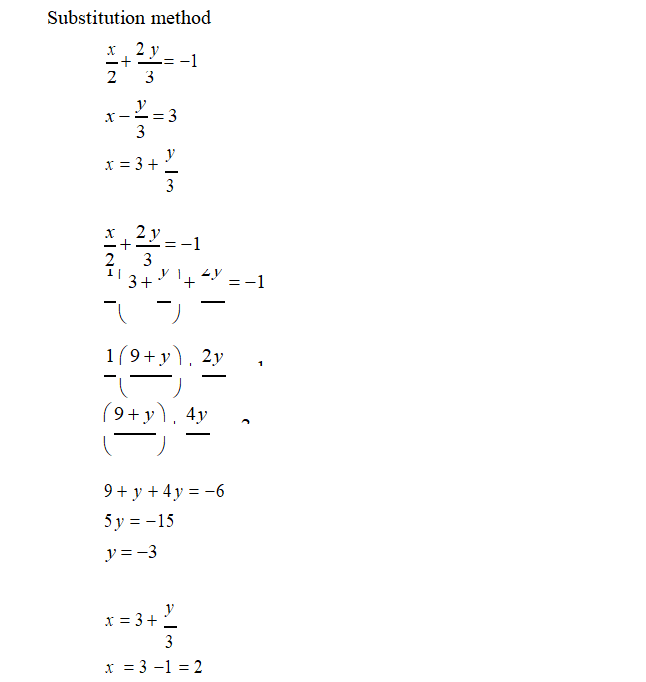
2. Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method :
(i) If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces to 1. It becomes 1/2 if we only add 1 to the denominator. What is the fraction?

(ii) Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu?
Let the present age of nuri = x
present age of sonu = y
As per the question
( x - 5) = 3( y - 5)
x - 3y = -10
( x +10) = 2( y +10)
x - 2 y = 10
On solving the above equations we got, age of nuri is 50 yrs and age of sonu is 20 yrs.
(iii) The sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
Let the unit digit = x
tens digit = y
Number = 10y+x
Number on reversal the digits = 10x + y
As per the question,
x + y = 9 ...1
9(10 y + x) = 2(10x + y )
-x + 8 y = 0 ...2
On adding the above equations, 9 y = 9
y = 1
x = 8
Number = 18
(iv) Meena went to a bank to withdraw ` 2000. She asked the cashier to give her ` 50 and ` 100 notes only. Meena got 25 notes in all. Find how many notes of ` 50 and ` 100 she received.
Let the number of Rs 50 notes = x the number of Rs 100 notes = y As per the question,
x + y = 25
50x +100 y = 2000
On solving above equations,
we got,
The number of Rs 50 notes = 10
The number of Rs 100 notes = 15
(v) A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid ` 27 for a book kept for seven days, while Susy paid ` 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day.
Let the fixed charge for first three days = Rs x
each day charge thereafter = Rs y
As per the question,
x + 4 y = 27
x + 2 y = 21
On subtraction,
2 y = 6
y = 3
x = 15
Thus, the fixed charge for first three days = Rs 15
each day charge thereafter = Rs 3
While referring to these NCERT Solutions, it's better to follow the latest NCERT Book for Class 10 Maths as the book has been revised and some topics and chapters have been kept out to reduce the syllabus load on students. Therefore, prepare for your board exams as per the content of the new NCERT Book.
Comments
All Comments (0)
Join the conversation