CBSE Class 10 Maths Chapter 3 Important Questions with Solutions: In this article we will cover all types of important questions from multiple choice question type, objective question type, short answer type, long answer type ands case study question type, along with their solutions. Students should use these as their preparation booster along with other resources for CBSE Class 10 Mathematics Board exams. With the help of these questions, students can master the variety of questions that can possibly be asked in exams and score excellently in CBSE Class 10 board exam 2022-23.
Chapter 3 Pair of Linear Equations in Two Variables comes under the Unit Algebra which carries 20 marks. It covers Pair of linear equations in two variables and graphical method of their solution, consistency/inconsistency. Algebraic conditions for number of solutions. Solution of a pair of linear equations in two variables algebraically - by substitution, by elimination. Simple situational problems.
| View and Download CBSE Class 10 Mathematics syllabus 2022-23 |
Let us now begin.
Important Questions from CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables
Related: CBSE Class 10 Maths Important Formulas for Last Minute Revision for Board Exam 2023
MULTIPLE CHOICE QUESTIONS
Q1. The pair of linear equations 3x + 5y = 3 and 6x + ky = 8 do not have a solution if k
a) = 5 b) = 10 c) ≠10 d) ≠ 5
Q2. The solution of the equation x + y = 5 and x − y = 5 is
a) (0,5) b) (5,5) c) (5,0) d) (10 ,5)
Q3. The pair of linear equations x = 0 , x = −5 has
a) One solution b) two solution c) infinite no: of solution d) no solution
Q4. For what value of ‘k’ do the equations 3x – y + 8 = 0 and 6x – ky + 16 = 0 represent coincident lines
a) 1/2 b) −1/2 c) 2 d) -2
Q5. The value of ‘k’ for which the system of equations 4x + ky + 8 = 0 and 2x + 2y + 2 = 0 has a unique solution is 35
a) k=3 b) k ≠ 4 c) k ≠ 0 d) k=0
OBJECTIVE TYPE QUESTIONS
Q1. In how many points do the lines represented by the equations x − y = 0 and x + y = 0
intersect?
Q2. Find the value of (x + y)if , 3x − 2y = 5 and 3y − 2x = 3
Q3. Sum of two numbers is 35 and their difference is 13, find the numbers
Q4. Find the value of ‘p’ for which the pair of linear equations 2px + 3y = 7: 2x + y = 6 has exactly one solution
Q5. Do the equations y = x and y = x + 3 represent parallel lines?
CASE STUDY BASED QUESTIONS
The alumni meet of two batches of a college- batch A & batch B were held on the same day in the same hotel in two separate halls “Rose” and “Jasmine”. The rents were the same for both the halls. The expense for each hall is equal to the fixed rent of each hall and proportional to the number of persons attending each meet. 50 persons attended the meet in “Rose” hall, and the organisers had to pay ₹ 10000 towards the hotel charges. 25 guests attended the meet in “Jasmine” hall and the organisers had to pay ₹ 7500 towards the hotel charges. Denote the fixed rent by ₹ x and proportional expense per person by ₹ y.
- Represent algebraically the situation in hall “Rose”.
a) 50x + y = 10000
b) 50x − y = 10000
c) x + 50y = 10000
d) x − 50y = 10000
2. Represent algebraically the situation in hall “Jasmine”
a) x + 25y = 7500
b) x − 25y = 7500
c) 25x + y = 7500
d) 25x − y = 7500
3. What is the fixed rent of the halls?
a) ₹2500
b) ₹3300
c) ₹ 4000
d) ₹5000
4. Find the amount the hotel charged per person.
a) ₹ 150
b) ₹ 190
c) ₹130
d) ₹ 100
SHORT ANSWER TYPE QUESTIONS (2 MARKS)
Q 1. Find the solutions of the pair of linear equations 5x + 10y – 50 = 0 and x + 8y = 10. Hence find the value of m if y = mx + 5.
Q 2. Are the following pair of linear equations consistent? Justify your answer.
2ax + by = a; 4ax + 2by – 2a = 0 ; a , b ≠ 0
Q 3. There are 20 vehicles – cars and motorcycles in a parking area. If there are 56 wheels together, how many cars and motorcycles are there?
Q 4. Write a pair of linear equations which has a unique solution x = 2 and y = −1. How many such pairs are possible?
Q 5. If the sum of two positive numbers is 108 and the difference of these numbers is 8, then find the numbers.
SHORT ANSWER TYPE QUESTIONS ( 3 MARKS)
Q1. Find the two-digit numbers whose sum is 75 and difference is 15
Q2. The monthly incomes of A and B are in the ratio 5:4 and their expenditure are in the ratio 7:5. If each saves 3000/- per month, find the monthly income of each.
Q3. A and B each have a certain number of oranges. A says to B, “if you give me 10 of your oranges, I will have twice the number of oranges left with you.” B replies,” if you give me 10 of your oranges, I will have the same number of oranges as left with you. Find the number of oranges with A and B separately.
Q4. Yash scored 40 marks in a test, receiving 3 marks for each correct answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each wrong answer, then Yash would have scored 50 marks. How many questions were there in the test?
Q5. A man has only 20 paisa coins and 25 paisa coins in his purse. If he has 50 coins in all totalling 11.25/-, how many coins of each kind does he have?
LONG ANSWER TYPE QUESTIONS (4 Marks)
Q1. Two numbers are in the ratio 5:6. If 8 is subtracted from each of the numbers, the ratio becomes 4:5. Find the numbers.
Q2. The age of the father is twice the sum of the ages of his two children. After 20 years, his age will be equal to the sum of the ages of his children. Find the age of the father.
Q3. A number consists of two digits. When the number is divided by the sum of its digits, the quotient is 7. If 27 is subtracted from the number, the digits interchange their places. Find the number.
Q4. Draw the graphs of 2x − 3y + 6 = 0 and 2x + 3y − 18 = 0. Find the ratio of areas of triangles formed by the given lines with X-axis and Y-axis.
Q5. Determine graphically the vertices of the triangle, the equations of whose sides are given below
2y − x = 8; 5y − x = 14; y − 2x = 1
| ALSO CHECK: CBSE Class 10 Mathematics Standard Sample Paper 2023 |
| ALSO CHECK: CBSE Class 10 Mathematics Basic Sample Paper 2023 |
ANSWER KEY
| Q no | MULTIPLE CHOICE QUESTIONS |
| 1 | b |
| 2 | c |
| 3 | d |
| 4 | c |
| 5 | b |
| Q no | OBJECTIVE TYPE QUESTIONS |
| 1 | one |
| 2 | X + Y = 8 |
| 3 | 24, 11 |
| 4 | P ≠ 3 |
| 5 | Yes |
CASE STUDY BASED QUESTIONS
Let us denote the fixed rent by ₹ x and proportional expense per person by ₹ y.
- Algebraic representation of the situation in “Rose” hall
x+50 y=10000
Answer- Option C
2. Algebraic representation of the situation in “Jasmine” hall
x+25y=7500
Answer- Option A
Subtracting the equations represented by (i) and (ii)
x+50y-x+25y=10000-7500
25y=2500
y=100
Substituting y=100 in x+50 y=10000, we get
x+50 x 100=10000
x+5000=10000
x=5000
3. Answer : Option D
4. Answer : Option D
SHORT ANSWER TYPE QUESTIONS (2 MARKS)
1 Solving 5x + 10y – 50 = 0
10 (x/2 + y - 5) = 0
y = 5 - x/2
Substituting y = 5 - x/2 in x + 8y = 10 we get
x + 8 (5 - x/2) = 10
x = 10
Thus y = 0
Substituting the values of x and y in y = mx + 5, we get
0 = m10+5
Therefore m = −1/2
2 The given pair of linear equation can be written as
2ax+by−a=0 and 4ax+2by−2a
Here,
a1=2a,
b1=b,
c1=−a
And a2=4a,
b2=2b,
c2=−2a
∴ a1/a2 = 2a/4a = 1/2 and b1/b2 = b/2b = 1/2 and c1/c2 = −a/−2a = 1/2
Since, a1/a2 = b1/b2 = c1/c2 = 1/2
∴ The given pair of linear equation is consistent.
3 Let no of cars = x and no of motorcycles = y
According to our condition
x + y = 20
X = 20 - y (i)
4x + 2y = 56 (ii)
Replacing (i) in (ii) we get
4(20 - y) + 2y = 56
80 - 4y + 2y = 56
-2y = -24
Thus y = 12
Now replacing y = 12 in x + y = 20 we get
x = 8
4 Condition for any pair of systems to have a unique solution is a₁/a₂ ≠ b₁/b₂
Let us consider the following equations
a₁x + b₁y + c₁ = 0 and
a₂x + b₂y + c₂ = 0
We have x = 2 and y = - 1 as the unique solution of these two equations.
Hence, it must satisfy the above equations
a₁(2) + b₁(- 1) + c₁ = 0
2a₁ - b₁ + c₁ = 0 ------------------------ (1)
a₂(2) + b₂(- 1) + c₂ = 0
2a₂ + -b₂ + c₂ = 0 ----------------------- (2)
the restricted values of a1,a2 and b1,b2 are only
a2a1=b2b1...(3)
So all the real values a1,a2,b1,b2 except condition (3) can from so many linear equations which will satisfy equation (1) and (2)
Therefore, infinitely many pairs of linear equations are possible.
Infinite number of solution.
5 According to the question
x + y = 108
So x = 108 - y
And x – y = 8
So 108 - y - y = 8
-2y = -100
y = 50
Thus x = 108 - 50 = 58
SHORT ANSWER TYPE QUESTIONS ( 3 MARKS)
1 Let the numbers be x and y.
x + y = 75
Thus x = 75 - y............(1)
x – y = 15............(2)
Substituting (1) in (2) 2y = 90
So y = 45.
Putting y = 45 in (1) , x= 30.
Hence the numbers are x = 30 and y= 45
2 By the given conditions
The monthly income would be 5x:4x and monthly expenditure would be 7y:5y
Since saving = income - expenditure
5x-7y=3000 ................(1)
4x-5y= 3000 ...............(2)
Solving, we get x= 2000/-
Monthly income of A = 5x= 5×2000= 10000/-
Monthly income of B = 4x = 4 × 2000 = 8000/-
3 Suppose A has x number of oranges and B has y oranges. Then
x +10 = 2( y-10)
⟹ x − 2y + 30 = 0
y + 10 = x − 10
⟹ x − y − 20 = 0
Equating both the equations we get y=50 and x=70
Hence A has 70 oranges and B has 50 oranges
4 Let right answer questions attempt by Yash be x and wrong answer questions be y
Then, 3x – y = 40.............(i)
4x - 2y = 50 ............(ii)
Solving we get x = 15, y = 5
Total number of questions in the test = x + y=15 + 5 = 20.
5 Let no. of 20 paisa coins be x and that of 25 paisa coins be y, then
x + y = 50 ...............(i)
20 x + 25y = 1125 ⟹ 4x + 5y = 225 ........... (ii)
Solving, we get x=25 and y=25
Hence there are 24 points of each kind.
LONG ANSWER TYPE QUESTIONS (4 Marks)
1 Let the two numbers be 5x and 6x
Then according to the question
5x-8 : 6x-8 = 4:5
Cross multiplying, we get
5( 5x-8 ) = 4 ( 6x-8 )
Solving this equation we get
x = 8
Replacing the value of x we get that the numbers are 40 and 48.
2 Let the present age of his two children be “x” years and “y” years.
Present age of father = 2(x+y)----(1)
Then, according to the question
2x+y+20=x+20+y+20
2x+2y+20=x+y+40
2x+2y-x-y=40-20
x+y=20 ----(2)
Substituting eqn (2) in eqn (1), we get
Present age of father = 2 x 20
= 40 years
3 Let the digit in ones place be y and the digit in tens place be y.
Then the two digit number = 10x+y
Given 10x+yx+y=7
⇒ 10x + y = 7 ( x + y )
∴ 10x+y-7x-7y=0
3x-6y=0
x-2y=0--------(1)
According to the second condition.
10x + y - 27 = 10y + x
10x+y-10y-x=27
9x-9y=27
x-y=3-------(2)
Equation (1)- equation (2)
x-2y-x-y=0-3
x-2y-x+y=-3
-y=-3
Thus y=3
Substituting y=3 in equation (2), we get
x-3=3
x=6
Since two-digit number =10x+y
So 10x6+3
=60+3=63
Then 20y + y - 27 = 10y + 2y
⇒ 9y = 27
⇒y = 3
Substitute y value in eqn(1)
we get, x = 2× 3
⇒ x = 6
Hence the required number is 63.
4 Find three solutions of 2x-3y+6=0
Find three solutions of 2x+3y-18=0
Plot the points on the graph paper.
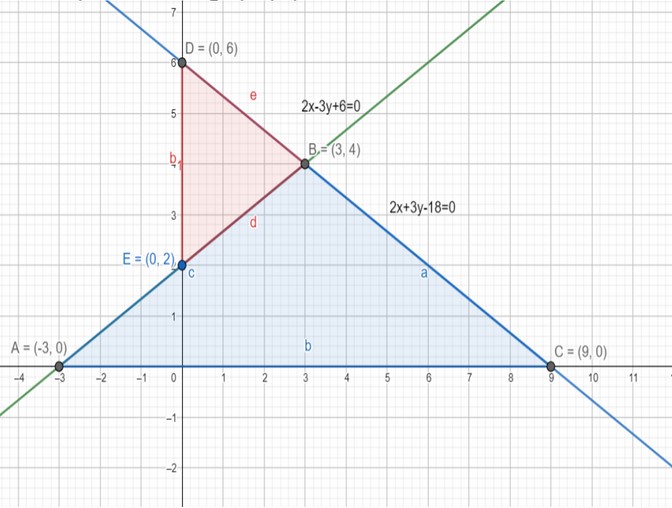
Area of triangle ABC formed by the lines and the X-axis
=12 x12 x4 =24 sq.units
Area of triangle DEB formed by the lines and the Y-axis
=12 x4x3 =6 sq.units
Ratio of areas of triangles formed by the given lines with X-axis and Y-axis =
24 : 6 = 4 : 1
5 Find three solutions of 2y-x=8
Find three solutions of 5y-x=14
Find three solutions of y-2x=1
Plot the points on the graph paper.
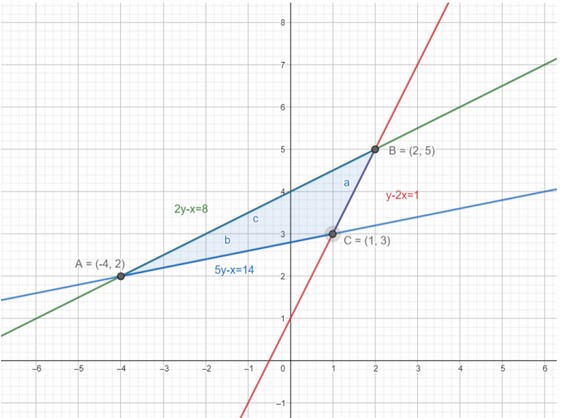
Coordinates of triangle ABC formed between the given lines A(-4,2), B (2,5),
C(1,3)
Pair of Linear Equations in Two Variables is the second chapter of the second unit.
The other chapters in Unit two Algebra of CBSE Class 10 Maths are Polynomials,, Quadratic Equations and Arithmetic Progressions.
All the best!
Related resources:
- CBSE class 10 Maths syllabus 2023
- NCERT Book for Class 10 Maths
- NCERT Solutions for Class 10 Maths
- NCERT Exemplar Solutions for Class 10 Maths
- CBSE Class 10 Maths Sample Paper 2023 (Standard)
- CBSE Class 10 Maths Sample Paper 2023 (Basic)
- Previous Year Questions of CBSE Class 10 Maths Standard
- CBSE Class 10 Maths Basic Previous Year Question Papers PDF Download
- CBSE Class 10 Maths Important Questions and Answers
- CBSE Class 10 Maths Topper Answer Sheet
- CBSE Class 10 Maths Important Formulas for Last Minute Revision
- CBSE Class 10 Maths Preparation Tips to Score 95+ Marks in CBSE Class 10 Maths Board Exam 2023
| Now test your preparation with these practise papers created by subject experts to prepare you for CBSE Class 10 Math Board Examination 2023.
|
Comments
All Comments (0)
Join the conversation