CBSE Class 9 Maths Sample Paper 2025: Download the Sample Question Paper with Solutions in PDF

The CBSE Class 9 Maths sample paper includes important questions based on the latest syllabus and exam pattern. Curated by experts, it helps students practice effectively, understand the marking scheme, and prepare thoroughly for the 2025 Annual Exam.

Feb 3, 2025, 14:10 IST

Download CBSE Class 9 Maths Sample Paper 2025 with Solutions

Class 9 Maths Sample Paper 2024-25: Looking for the perfect resource to prepare for the CBSE Class 9 Maths Annual Exam 2025? This article provides a comprehensive sample paper designed by experienced faculty, featuring important questions and detailed solutions to boost your confidence. Based on the latest CBSE syllabus and exam pattern, this sample paper helps students understand the marking scheme and question format. Download the CBSE Class 9 Maths sample paper with solutions to practice effectively, strengthen your concepts, and ace your exams with ease.

General Instructions for Students

Read the following instructions carefully and follow them while practising with the sample paper provided in this article:

This paper contains 38 questions, divided into 5 Sections A, B, C, D and E.
In Section A, question no. 1-18 are multiple choice questions (MCQs) and questions no. 19and 20 are Assertion- Reason based questions of 1 mark each.
In Section B, question no. 21-25 are short answer – I (SA-I) type questions, carrying 02 marks
In Section C, question no. 26-31 are short answer – II (SA-II) type questions, carrying 03 marks each.
In Section D, question no. 32-35 long answer – II (LA) type questions, carrying 05 marks each.
In Section E, question no. 36-38 are case study based questions carrying 4 marks each with sub parts of the values of 1, 1 and 2 marks each respectively.
All questions are compulsory. However, an internal choice in 2 Questions of section B, 2Questions of section C and 2 Questions of section D has been provided. And internal choice has been provided in all the 2 marks questions of Section E.
Draw neat and clean figures wherever required.
Take π =22/7 wherever required if not stated.

CBSE Class 9 Maths Syllabus 2024-2025 PDF

CBSE Class 9 Maths Deleted Syllabus 2024-2025

CBSE Class 9 Maths Sample Paper 2024-25

Check and download the sample paper below to prepare effectively for the CBSE Class 9 Maths Annual Exam 2024-25:

Section A

1. The number obtained on rationalizing the denominator of 1/(√7 – 2) is________

Answer: Option (d)

2. Between two rational numbers __________

a) there are only rational numbers and no irrational number

b) there are infinitely many rational numbers

c) there is exactly one rational number

d) there is no rational number

Answer: b) there are infinitely many rational numbers

3. The value of the polynomial 5x − 4x² + 3 , when x = −1 is ______

a) − 6

b) 6

c) 1

d) − 1

Answer: a)− 6

4. The factorization of 4x² + 8x + 3 is___________

a) (2x – 1) (2x – 3)

b) (2x + 2) (2x + 5)

c) (x + 1) (x + 3)

d) (2x + 1) (2x + 3)

Answer: d) (2x + 1) (2x + 3)

5. The linear equation 3x – y = x – 1 has__________

a) A unique solution

b) Two solutions

c) No solution

d) Infinitely many solutions

Answer: d) Infinitely many solutions

6. The graph of the linear equation y = x passes through the point_______

Answer: d) (1, 1)

7. Point (–3, 5) lies in the_________

a) second quadrant

b) fourth quadrant

c) third quadrant

d) first quadrant

Answer: a) second quadrant

8. If the y co-ordinate of a point is zero, then this point always lies_____

a) in quadrant I

b) on y - axis

c) on x - axis

d) in quadrant II

Answer: c) on x - axis

9. The angles of a triangle are in the ratio 5: 3: 7, the triangle is_____

a) An isosceles triangle.

b) An obtuse angled triangle

c) A right triangle

d) An acute angled triangle

Answer: d) An acute angled triangle

10. In the given figure (not drawn to scale), if AB || CD, then x and y respectively are ____.

a) 40°, 30°

b) 30°, 45°

c) 90°, 30°

d) 50°, 77°

Answer: d) 50°, 77°

11. It is given that △ ABC ≅ △ FDE and AB = 5 cm, ∠ B = 40° and ∠ A = 80°. Then which of the following is true?

a) DE = 5 cm, ∠ E = 60°

b) DF = 5 cm, ∠ E = 60°

c) DF = 5 cm, ∠ F = 60°

d) DE = 5 cm, ∠ D = 40°

Answer: b) DF = 5 cm, ∠ E = 60°

12. ABCD is a Rhombus such that ∠ ACB = 40°, then ∠ ADB is______

a) 100°

b) 40°

c) 60°

d) 50°

Answer: d) 50∘

13. Diagonals of a Parallelogram ABCD intersect at O. If ∠ BOC = 90°, ∠ BDC = 50°, then ∠ OAB is _______

a) 10°

b) 40°

c) 90°

d) 50°

Answer: b) 40∘

14. The sides of a triangle are 56 cm, 60 cm and 52 cm long. Then the area of the triangle is ___________

a) 1311cm²

b) 1344cm²

c) 1322cm²

d) 1392cm²

Answer: b) 1344cm²

15. In the given figure, AB = 8 cm, OM = ON = 4 cm. Then CD is ________.

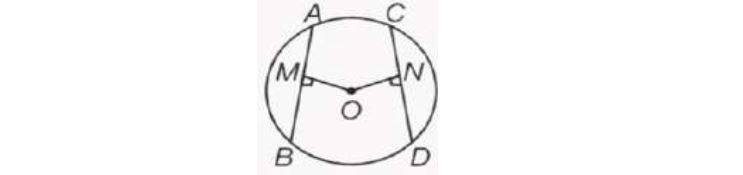
a) 3.5 cm

b) 4.5 cm

c) 8 cm

d) 3 cm

Answer: c) 8 cm

16. In the given figure, ∠ ABD = 70°, ∠ ADB = 30°. Then, ∠ BCD is ________.

a) 100°

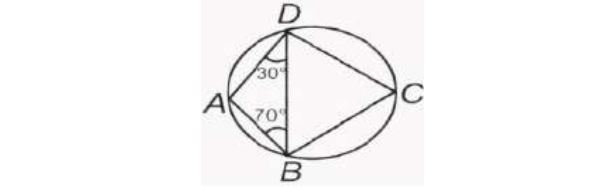
b) 90°

c) 120°

d) 80°

Answer: a) 100°

17. If the TSA of a solid hemisphere is 12π sq. cm, then its CSA is______

a) 16π sq. cm

b) 12π sq. cm

c) 24π sq. cm

d) 8π sq. cm

Answer: d) 8π sq. cm

18. To draw a histogram to represent the following frequency distribution, the adjusted frequency for the class 25 - 45 is________

Class	5 – 10	10 – 15	15 – 25	25 – 45	45 – 75
Frequency	6	12	10	8	15

a) 6

b) 5

c) 2

d) 3

Answer: c) 2

19. Assertion (A): The point (2, −3) lies on the on the line x + y = 5.

Reason (R): A point which satisfies the linear equation lies on the line representing it.

a) Both A and R are true and R is the correct explanation of A.

b) Both A and R are true but R is not the correct explanation of A.

c) A is true but R is false.

d) A is false but R is true.

Answer: d) A is false but R is true.

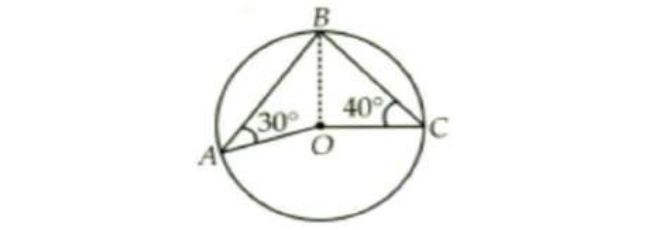
20. Assertion (A): The measure of ∠ AOC = 60° Reason (R): Angle subtended by an arc of a circle at the centre of the circle is double the angle subtended by arc on the circumference.

a) Both A and R are true and R is the correct explanation of A.

b) Both A and R are true but R is not the correct explanation of A.

c) A is true but R is false.

d) A is false but R is true.

Answer: d) A is false but R is true.

Section B

21.State the quadrants of the following points:

(i) A (-4, 3)

(ii) B (-5, -3)

(iii) C (5, 4)

(iv) D (-4, 4)

Solution:

(i) A (-4, 3) - II Quadrant

(ii) B (-5, -3) - III Quadrant

(iii) C (5, 4) - I Quadrant

(iv) D (-4, 4) - II Quadrant

22.In fig., if AC = BD, then prove that AB = CD

Solution:

AC = BD [Given] . . . (i)
AC = AB + BC [Point B lies between A and C] . . . (ii)
BD = BC + CD [Point C lies between B and D] . . . (iii)
Substituting (ii) and (iii) in (i), we get,
AB + BC = BC + CD
AB = CD [Subtracting equals from equals]

23.The height and the slant height of a cone are 21 cm and 28 cm respectively. Find the volume of the cone.

Solution:

Given, For Cone, h = 21 cm and l = 28 cm
We know, l² = r²+ h²
⇒ (28)²= r² + (21)²
⇒ r² = 343
⇒ r = 7√7 cm
Now, Volume of Cone = 1/3πr²ℎ
=1/3 × 22/7 × 7√7 × 7√7 × 21
= 7546 cm³

23.Find the curved surface area of a right circular cone whose height is 15 cm and base radius is 8 cm. (Use π = 22/7)

Solution:

Given, For Cone, h = 15 cm and r = 8 cm
We know, l²=r² + hπ²
⇒ l² = (8)² + (15)²
⇒ l² = 289
⇒ l = 17 cm
Now, CSA of Cone = rl
= 22/7 × 8 × 17
= 427.42 cm²

24.If the volume of a right circular cylinder of height 9 cm is 49πcm3, find the diameter of its base.

Solution:

Given, For Cylinder, h = 9 cm and volume of cylinder = 49π cm³

Now, Volume of Cylinder = πr²h

⇒ 49π = π × r² × 9

⇒ r² = 49/9

⇒ r = 7/3

⇒ d = 14/3

⇒ d = 4.66 cm

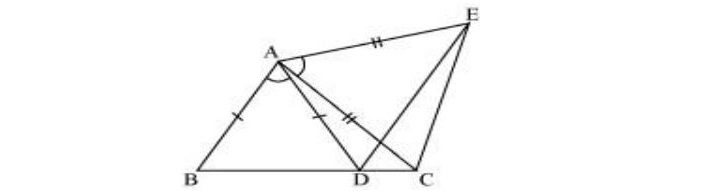
25.In figure, AC = AE, AB = AD and∠ BAD = ∠ EAC. Show that BC = DE.

Solution:

∠BAD = ∠EAC [Given]

⇒ ∠BAD + ∠DAC = ∠DAC + ∠EAC [Adding ∠DAC to both sides]

⇒ ∠BAC = ∠DAE … (i)

In ∆ ABC and ∆ ADE,

AC = AE [Given]

∠BAC = ∠DAE [From (i)]

AB = AD [Given]

∆ ABC ≅ ∆ ADE [By SAS congruence

⇒ BC = DE [CPCT]

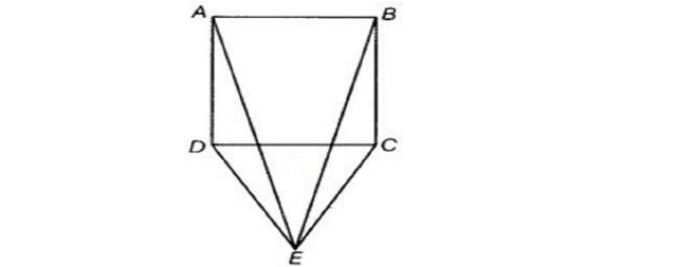
25.CDE is an equilateral triangle formed on a side CD of a square ABCD (Fig.). Show

that, △ ADE ≅ △ BCE.

Solution:

∠ADC = ∠BCD [Angles of a square] …(i)

∠CDE = ∠DCE [Angles of an equilateral triangle] …(ii)

Adding (i) and (ii) we get,

∠ ADE = ∠BCE …(iii)

In △ ADE and △ BCE,

AD = BC [sides of square]

∠ ADE = ∠BCE …[from (iii)]

DE = CE [sides of equilateral triangle )

⇒ △ ADE ≅△ BCE [SAS Criteria]

Section C

26.Locate √10 on the number line.

27.Factorize: 3x²− x − 4

28.Find 3 solutions for the linear equation 2x – 3y + 7 = 0.

29.In figure, if PQ || RS,∠ MXQ = 135° and ∠ MYR = 40°, find ∠XMY.

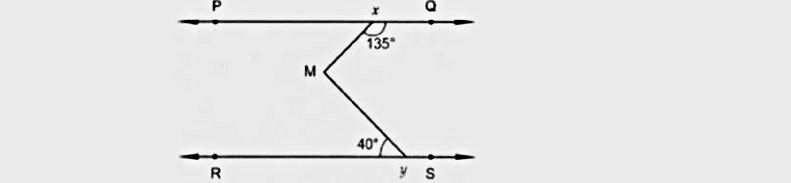
In figure, if PQ || ST, ∠ PQR = 110o and ∠ RST = 130o,find ∠QRS.

30.In the given figure, the side BC of △ ABC has been produced to a point D. If the bisectors of ∠ ABC and ∠ ACD meet at point E then prove that ∠ BEC = 1/2∠ BAC.

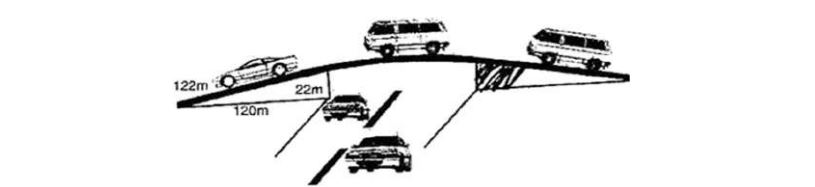
31.The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see figure). The advertisements yield earnings of ₹ 5000 per m² per year. A company hired one of its walls for 3 months. How much rent did it pay?