Prime Numbers: Definition, Properties, Examples, Applications and FAQs

Prime Numbers: Prime numbers are fundamental building blocks in number theory. They are the essential ingredients for understanding various mathematical concepts like divisibility, factorization, and cryptography. The concept is important for students of all standards This concept is important for students of all standards as it lays the foundation for more advanced mathematical topics and applications. This article explains everything you need to know about prime numbers, starting from their definition and properties to their applications in various fields.

Major concepts discussed in this article include:

Definition of Prime Numbers
Examples of Prime Numbers
Properties of Prime Numbers
Difference Between Prime Numbers and Composite Numbers
Identification of Prime Numbers
List of Prime Numbers from 1 to 1000
Solved Questions
Applications of Prime Numbers
Frequently Asked Questions

Definition of Prime Numbers

A prime number is a natural number greater than 1 that has exactly two distinct factors, 1 and the number itself. So, if p is a prime number then its only factors will be 1 and p itself.

Examples:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ... (the list continues infinitely)

Pythagoras Theorem: Definition, Formula, Proof, Examples and Applications

Sequence and Series: Formula, Definition & Concepts

Composite Numbers

Composite numbers can be defined as natural numbers with more than two factors.

Examples:

4: It can be formed by multiplying 2 x 2, so it's a composite number (not prime).
9: It can be factored as 3 x 3, making it composite.

Properties of Prime Numbers

All prime numbers are odd except 2.
There are infinitely many prime numbers.
Aprime number cannot be formed by multiplying two smaller natural numbers.
Every number greater than 1 can be divided by at least one prime number.
Every even positive integer greater than 2 can be expressed as the sum of two prime numbers.
Any two prime numbers are always coprime to each other, i.e., they that do not have any common factor other than 1.
Each composite number can be factorised into prime factors.

How to Identify Prime Numbers?

Various methods of identifying prime numbers are explained below in a step-wise manner:

1. Finding Prime Numbers Using Factorization

Factorisation is the simplest way to find prime numbers. The method can be used to identify prime numbers as follows:

(i) First find the factors of the given number.

(ii) Check the number of factors taken out for that number.

(iii) If the number of factors is more than two then the given number not a prime number. It is a composite number.

Example 1: Find out if 42 is a prime number or not.

Solution: Here, 42 can be written as 2 × 3 × 7. Since, the factors of 42 are more than two, it is not a prime number but a composite number.

Example 1: Find out if 17 is a prime number or not.

Solution: The prime factorisation of 17 is 1 x 17. Thus, there are two factors of 17, 1 and the number 17 itself. Hence, it is a prime number.

2. Identifying Large Numbers as Prime Numbers

We can use some general facts and Prime Number Formulas to find the primes. To check whether a large number is a prime number or not, follow the steps given below:

(i) Unit Place: Check the unit place of the given number. Numbers ending with 0, 2, 4, 6 and 8 are not prime numbers.

(ii) Sum of all digits: If the above step fails then take the sum of the digits of the given number. If the sum of all digits is divisible by 3 then the number is not a prime number.

(iii) Square root method: If both steps 1 and 2 violate then use the square root method as mentioned below:

Find the square root of the given number.
Divide the given number by all the prime numbers below its square root value.
If the number is divisible by any of the prime numbers less than its square root then it is not a prime number.

List of Prime Numbers from 1 to 100

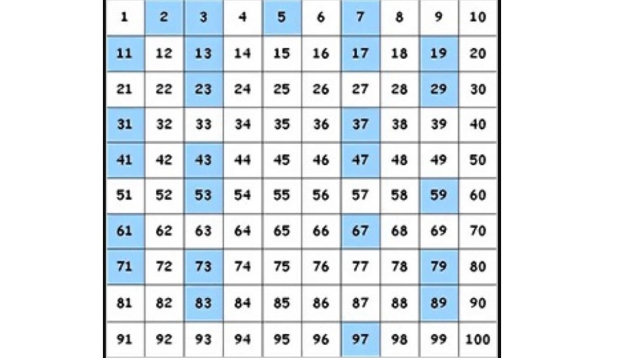
Check the table below for prime numbers lying between 1 to 100:

2	3	5	7
11	13	17	19
23	29	31	37
41	43	47	53
59	61	67	71
73	79	83	89
97

List of Prime Numbers from 1 to 1000

2	3	5	7	11	13	17	19	23	29
31	37	41	43	47	53	59	61	67	71
73	79	83	89	97	101	103	107	109	113
127	131	137	139	149	151	157	163	167	173
179	181	191	193	197	199	211	223	227	229
233	239	241	251	257	263	269	271	277	281
283	293	307	311	313	317	331	337	347	349
353	359	367	373	379	383	389	397	401	409
419	421	431	433	439	443	449	457	461	463
467	479	487	491	499	503	509	521	523	541
547	557	563	569	571	577	587	593	599	601
607	613	617	619	631	641	643	647	653	659
661	673	677	683	691	701	709	719	727	733
739	743	751	757	761	769	773	787	797	809
811	821	823	827	829	839	853	857	859	863
877	881	883	887	907	911	919	929	937	941
947	953	967	971	977	983	991	997

Some Interesting Facts Regarding Prime Numbers

Smalest Prime Number: 2 is the smallest prime number.
Largest Prime Number: 2^82,589,933− 1 is the largest prime number. It that has 24,862,048 digits when written in base 10.
Even Prime Number: The only even prime number is 2.
Twin Prime Numbers: The prime numbers with only one composite number between them are called twin prime numbers or twin primes. For example, 3 and 5, 5 and 7, 11 and 13, 17 and 29, etc.
Coprime Numbers: the set of numbers that only share the number 1 as a common factor are called coprime numbers. For example, 6 and 13 are coprime because the common factor is 1 only.
Twisted Prime Number: A number is said to be twisted prime if it is a prime number and its reverse is also a prime number. For example, 17 and 71, 79 and 97.

Applications of Prime Numbers

Prime numbers have numerous practical applications that touch various aspects of our digital world. Some of the most common fields relying upon the applications of prime numbers include:

Foundation of Number Theory: Prime numbers are the building blocks for understanding factorization, a crucial concept in mathematics. Every natural number can be expressed as a unique product of prime numbers (Fundamental Theorem of Arithmetic).
Cryptography: One of the most crucial applications of prime numbers is in cryptography, where they are employed to protect sensitive information, including banking transactions, email communications, and military secrets. The security of these systems depends on the challenge of factoring large composite numbers into their prime factors. The larger the prime factors, the more secure the system becomes, making prime numbers vital for securing our digital world.
Pseudorandom Number Generation: Prime numbers are used in generating pseudorandom numbers, which are essential for simulations, computer games, and various algorithms.
Music: Prime numbers have also influenced the world of music, where they are used to craft distinctive rhythms and harmonies. For instance, the Fibonacci sequence, which is closely associated with prime numbers, has been utilized to generate musical patterns that are pleasing to the ear.

In conclusion, prime numbers are fascinating mathematical entities with unique properties which have led to many practical applications in our daily lives. Understanding their properties and behaviour is crucial for various mathematical disciplines and their role in the technological advancements of the modern world.

Also Read

Video Courses for PCMB (Class 10 and 12)

You can now access video lectures designed by experts for major topics of Physics, Chemistry, Maths and Biology to get a better concept clarity and achieve success in your academics. Find the video link below:

Comments

All Comments (0)

Join the conversation

Prime Numbers: Definition, Properties, Examples, List Upto 1000, Applications and FAQs

Prime Numbers: Prime numbers are a fundamental concept in number theory. This article explores the definition of prime numbers, list of 1 to 1000 prime numbers, solved questions, applications and frequently asked questions regarding prime numbers.