AP Inter 2nd Year Mathematics Paper- IIA Exam 2025: Candidates can find a detailed exam analysis for the AP Inter 2nd Year Mathematics Paper- IIA exam on this page. The exam ended at 12 PM. This analysis includes the overall difficulty level of the paper and the difficulty level of each section – Section A, Section B, and Section C.
It will also provide an idea of the expected good score, helping students assess their performance. Additionally, student reviews and feedback will be collected and updated here. These reviews will give valuable insights into the question paper, helping students understand the exam better.
AP Inter 2nd Year Mathematics Paper- IIA Question Paper 2025
AP Inter 2nd Year Mathematics Paper- IIA Question Paper 2025, will be provided soon
AP Inter 2nd Year Mathematics Paper- IIA Exam Analysis 2025
Here is theAP Inter 2nd Year Mathematics Paper- IIA Answer Key 2025 Exam Analysis 2025 in a tablulated information:
| Particulars | Details |
|---|---|
| Overall difficulty level of the exam | To Be Updated |
| Complexity level of Section A | To Be Updated |
| Complexity level of Section B | To Be Updated |
| Complexity level of Section C | To Be Updated |
| Was the exam time-consuming? | To Be Updated |
| Expected good score | To Be Updated |
AP Inter 2nd Year Mathematics Paper- IIA Answer Key 2025
Section A
1. Write the conjugate of the complex number 5i/(7+i).
Solution:
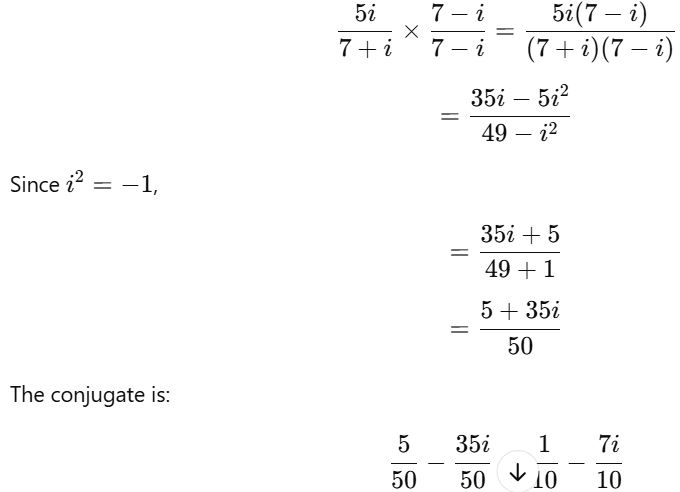
So, answer is 1/10−7i/10
2. Simplify -2i(3+i)(2+4i)(1+i)and obtain the modulus of that complex number.
Solution:
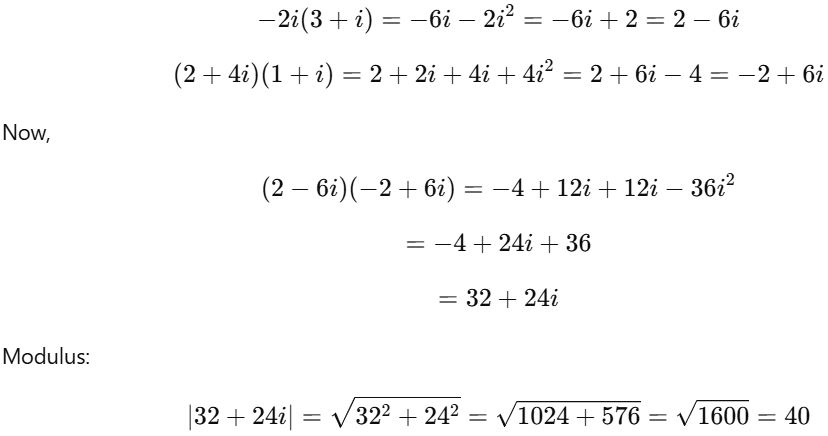
So, answer is 40.
3.If 1, ω, ω2 are the cube roots of unity, then prove that:
(2−ω)(2−ω2)(2−ω10)(2−ω11)=49
Solution:
We know that:
ω3=1,ω4=ω,ω5=ω2,…
Hence,ω10=ω,ω11=ω2
The equation becomes:
(2−ω)(2−ω2)(2−ω)(2−ω2)
Grouping the terms:
[(2−ω)(2−ω2)]2
Expand:
=(4−2ω−2ω2+ωω2)2
=(4−2ω−2ω2+1)2
=(5−2ω−2ω2)2
As 1+ω+ω2=0,
(5−2ω−2ω2)2= [5+2(1)]2=72=49
So, answer is 49
4.For what values of x the expression x2−5x−14 is positive?
Answer:
x2−5x−14>0
x2−7x+2x−14>0
(x−7)(x+2)>0
⇒x<−2 or x>7
Hence for x∈(−∞,−2)∪(7,∞), the expression x2−5x−14 is positive.
5. Form polynomial equations of the lowest degree, with roots 1, -1, 3.
Answer:
The polynomial equation with given roots is:
p(x)=(x−1)(x+1)(x−3) or simplifying this we get:
p(x)=x3−3x2−x+3
So, the required polynomial equation is p(x)=x3−3x2−x+3.
6.There are 4 copies (alike) each of 3 different books. Find the number of ways of arranging these 12 books in a shelf in a single row.
Answer:
Total books = 12 (4 copies each of 3 different books)
Total number of ways for arranging alike objects is
9. Find the mean deviation about the median for the following data: 4, 6, 9, 3, 10, 13, 2.
Answer:
Arrange data: 2, 3, 4, 6, 9, 10, 13
Median = 6
Mean deviation:
AP Inter 2nd Year Mathematics Paper- IIA Complete Answer Key 2025, will be provided soon
Also Check|
AP Inter 2nd year English Paper II Question Paper And Answer Key 2025

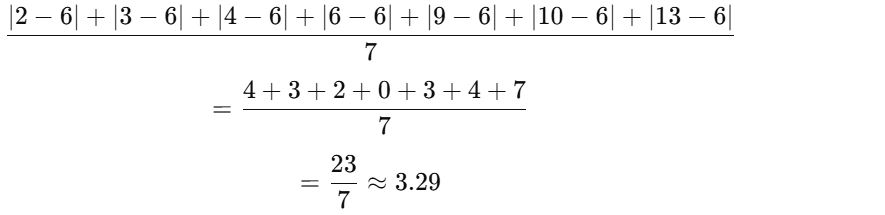
Comments
All Comments (0)
Join the conversation