ICSE Class 10 Maths Sample Paper: Preparing for the ICSE Class 10 Half Yearly Exams 2025-26 becomes easier with expert-curated sample papers. To help students strengthen their preparation for the Maths exam, we bring you the ICSE Class 10 Maths Half Yearly Sample Paper 2025, designed by subject experts. This paper includes important questions based on the latest ICSE Class 10 Maths syllabus and is structured as per the updated exam pattern. Practising this sample paper will help students:
-
Understand the latest paper pattern and marking scheme for half yearly exams.
-
Get familiar with the question format (MCQs, short answers, and long questions).
-
Revise important and high-weightage topics picked from the syllabus.
-
Enhance problem-solving speed and accuracy for the actual exam.
This model paper is a perfect practice set for students who wish to boost their confidence and score well in the upcoming half yearly examinations. Download the complete ICSE Class 10 Half Yearly Sample Paper 2025 in PDF for effective revision.
Also Check ICSE Class 10 Maths Syllabus 2025-2026
ICSE Class 10 Half Yearly Maths Sample Paper 2025
(Attempt all questions as per the instructions. Full paper is given below for practice.)
Full Marks – 80
Time - 3 Hours + 15 Min
Section A (Marks 40)
(Attempt All Questions)
Q1. Choose the correct answers to the questions from the given options [15]
i) A polynomial in ‘x’ is divided by (x-a) and for (x-a) to be a factor of this polynomial , the remainder should be
(a) -a
(b)0
(c)a
(d) 2a
ii) If sin A + cos A = √3 then find the value of ( tan A+ cot A)
(a) 1
(b)-2
(c)2
(d) None
iii) The Minimum value of x for the inequation 5x - 4 ≥ 18 - 6x
(a) 2
(b)22
(c)-22
(d) -2
iv) The Order of matrix A is 2 X 3 and that of B is 3 X 1.
(a) AB is possible , but BA is not possible
(b) BA is possible but AB is not possible
(c) AB as well as BA are not possible
(d) AB as well as BA are possible
v) The sum of first 10 even natural number is
(a) 120
(b)110
(c)65
(d) 120
vi) In a cylinder is radius is halved and height is doubled then the volume will be
(a) same
(b) doubled
(c) halved
(d) four times
vii) In triangle ABC, ∠BAC= 90° and AD is perpendicular to side BC. Triangle ABD is similar to triangle CBA by
(a)SAS
(b)ASA
(c)AAA
(d) RHS
viii) Which of the following equation represents a line equally inclined to the axes?
(a) 2x -5y +7 = 0
(b)x – y =6
(c)x= 7
(d) y= -7
ix) An article cost is x rupees and is sold at the profit of x% if it selling price is 56 the cost price is
(a) Rs 60
(b)Rs 50
(c)Rs 28
(d) Rs 40
x) The cost of certain services is Rs 10000 excluding GST = Rs 1800 The rate of GST is
(a)12%
(b)5%
(c)18%
(d)28%
xi) Given the numbers 10,12,14,16,17,x, in ascending order, if the mean and median of these observations are the same, what is the value of x?
(a)16
(b)17
(c)14
(d) 15
xii) If the length of the shadow of a pole is equal to its height then the angle of elevation of sun is
(a) 30°
(b) 45°
(c) 60°
(d) 90°
xiii) Assertion (A): The annual profit distributed among the share holders is called dividend
Reason (R): Dividend is always paid on the market value of a share.
(a) A is true , R is false
(b) A is false , R is true
(c) Both A and R are true , and R is the correct reason for A
(d) Both A and R are true , and R is incorrect reason for A
xiv) In the given figure O is the center of the circle and ∠B= 55°, Then the value of ∠A is:
(a) 55°
(b) 35°
(c) 45°
(d) 50°
xv) The incenter of a triangle is the point of intersection of which of the following?
(a) Perpendicular bisectors of its sides
(b) Angle bisectors of its angles
(c) A perpendicular to one side and an angle bisector
(d) None of these
Q2. a) Amit and Richa invest ₹12,000 each in buying shares of two companies. Amit buys 15% ₹100 shares at a discount of ₹20, while Richa buys ₹25 shares at 20% premium. If both receive equal dividends at the end of the year, find the rate percent of the dividend declared by Richa’s company. (4)
b) Prove that (1+cot A+tan A)(sin A−cos A) = (secA/cosec2A)-(cosecA/sec2A) (4)
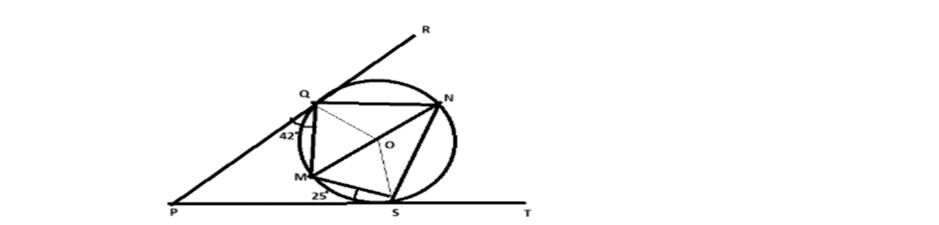
c) In the given diagram, O is the center of the circle, and PR and PT are two tangents drawn from the external point P, touching the circle at points Q and S respectively. MN is the diameter of the circle.Given that ∠PQM=42° and ∠PSM=25°, find the values of
i. ∠OQM ii.∠QNS iii∠QOS iv∠QMS (4)
Q3. a) Find the value of the middle most term of AP and Sum of the series
-11, - 7, - 3, …………. 49 (4)
b) Find the area of the Canvas required to make a conical tent 14 m high and 96 m in diameter given that
i.20% of the Canvas used in folds &stitching
ii. CSA of the tent (4)
c) Use graph paper for the question
i. Plot the points A (0,5) ,B(2,5),C(5,2),D(5,-2),E(2,-5)and F(0,-5)
ii. Reflect B,C,D and E On Y axis & name it B′,C′,D′ and E ′
iii. Write Coordinates of it B′,C′,D′ and E ′
iv. Write the geometrical name of BCDEE′D′C′B′ (5)
Section B (40 Marks)
(Attempt any Four questions Only)
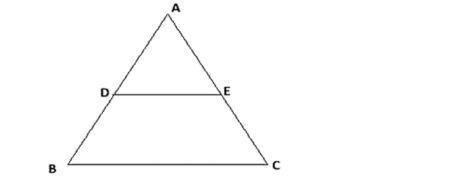
Q4. a) In the given figure, DE∥ BC, and If AD=4x−3 , AE= 8x-7 ,BD=3x−1 , EC=5x−3. Find the value of x , and the lengths of AB and AC (3)
b) Rohan has a four-year time deposit account and deposits ₹650 per month. If he receives ₹36,296 at the time of maturity, find the rate of interest. (3)
c) Find the mean of the following distribution by Step deviation method (4)
| CI | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| Frequency | 10 | 6 | 8 | 12 | 5 | 9 |
Q5. a) If the polynomial 2x3+ax2+bx−2 has a factor (x+2) and leaves a remainder of 7 when divided by 2x−3, find the values of a and b. With these values of a and b, factorize the given polynomial completely. (3)
b) Solve the following in equation and write the solution set
11x – 4 <15x + 4 <13x+8 , x€W
Represent the solution on a real number line (3)
c) A straight line passes through the points P(−1,4) and Q(5,−2). It intersects the coordinate axes at points A and B. M is the midpoint of the segment AB. Find
i. The equation of the line.
ii. Find the coordinates of points A and B.
iii. Find the coordinates of M. (4)
Q6. a) Find the equation of a line parallel to 2x+y−7=0 and passing through the intersection of x+y−4=0 and 2x−y=8. (3)
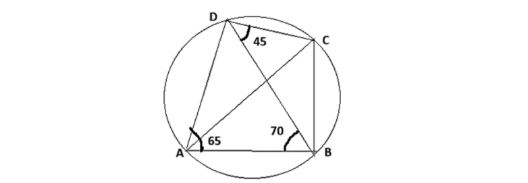
b) In the following figure, ∠BAD=65°, ∠ABD=70° and ∠BDC=45°
Find i) ∠BCD ii) ∠ADB
Hence prove that AC is a diameter of the circle. (3)
c) If the rate of GST is 12% and Mr. Atul has to pay ₹6000 including GST for an article, what amount he has to pay if the GST is increased by 6% by the government, Also find difference in GST amount ? (4)
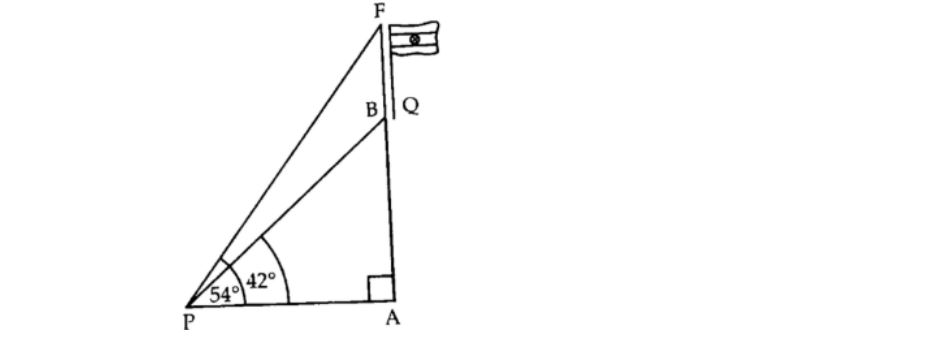
Q7. a) A vertical tower standing on a horizontal plane is surmounted by a vertical flagstaff at a point 100 m away from the foot of the tower, the angle of elevation of the top and bottom of the flagstaff is 54° and 42°, respectively.
Find the height of the flagstaff, correct to the nearest meter. (5)
b) Using graph paper, draw an ogive for the following data of scores obtained by 120 shooters in a shooting competition :
| Score Obtained | Number of Shooters |
| 0-10 | 5 |
| 10-20 | 9 |
| 20-30 | 16 |
| 30-40 | 22 |
| 40-50 | 26 |
| 50-60 | 18 |
| 60-70 | 11 |
| 70-80 | 6 |
| 80-90 | 4 |
| 90-100 | 3 |
i) Estimate the median from the graph.
ii)Interquartile Range
iii)The number of shooters who obtained more than 75% scores (5)
Q8.
Find the value of x and y (3)
b) A two-digit number is such that the product of its digits is 14. If 45 is added to the number, then the digits are interchange their places. Find the number. (3)
c) Construct a circle of radius 3.5 cm. Mark a point P outside the circle, at a distance of 6 cm from the center of the circle. Construct two tangents from P to the circle and measure the length of one tangent. (4)
Q9. a) The weekly pocket money of 50 students in a school is as follows:
| Weekly Pocket Money ( in Rs) | 40-50 | 50-60 | 60-70 | 70-80 80-90 90-100 | ||
| No of Students | 2 | 8 | 12 | 14 | 8 | 6 |
Construct a histogram using graph paper and estimate the mode from the graph. (3)
b) How many terms of the arithmetic progression 24, 21, 18, … must be taken so that the sum is 78? (3)
c) Solve the quadratic equation and give your answer correct to two decimal places. 5x(x+2) = 3. (4)
Q10. a) Two dice are rolled together. Find the probability of Getting:
i. A doublet
ii. atleast a 6
iii. A sum less than or equal to 12 (3)
b) In △ABC , the centroid G has coordinates (4,3) ,If the coordinates of two vertices A(1,3) and B(4,b), C(a, 1) , find a and b. Also find the length of side BC. (3)
c) A metal cube is completely submerged in water contained in a cylindrical vessel with a diameter of 30 cm, the water level rises by 1(41/99) cm.
i. Find the length of the edge of the cube
ii. the total surface area of the cube. (4)
Download ICSE Class 10 Half Yearly Maths Sample Paper 2025 PDF
The ICSE Class 10 Half Yearly Maths Sample Paper 2025 is an excellent resource for students to practice important questions and understand the latest exam pattern. By solving this paper, students can boost their confidence, improve time management, and revise key topics effectively. Make sure to attempt the complete paper in a timed manner for best results.
Download the PDF provided above and start your preparation today to score high in the upcoming half yearly exams!
Also Check ICSE Class 10th Maths Question Paper 2025

Comments
All Comments (0)
Join the conversation