NCERT Solutions For Class 10 Maths Chapter 2 Polynomial, Download PDF

NCERT Solutions for Class 10 Maths Chapter 2, Polynomials: Practicing NCERT questions will help students build their understanding and problem-solving skills. These questions are also important from the exam point of view as many times the questions have been asked directly and indirectly in the CBSE Board Exams. In this article, we have provided the NCERT solutions for Class 10 Math Chapter 2 - Polynomials. 

You will get the step-by-step solutions to the questions given in the chapter 2 - Polynomials. This helps students to understand the application of concepts and how to approach different types of questions in the examination. All the solutions have been collated in PDF format which students can easily download for free and start practicing for their board exam and score well. 

NCERT Solutions of Polynomials are as follows:

Find the complete solutions of all the exercise questions step-by-step, to get all the solutions in the PDF format click the link below and download the complete solutions. 

Exercise 2.1

1. The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.

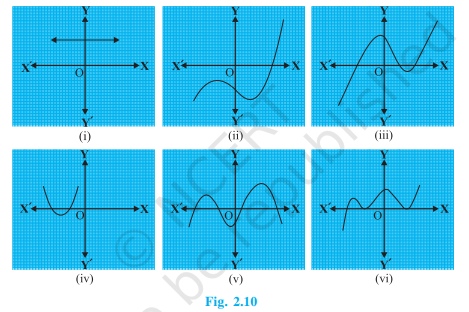
i) No. of zeroes=0 as graph doesn’t intersect at x-axis

ii) No. of zeroes =1 as graph intersect x-axis once

iii) No. of zeroes =3 as graph intersect x-axis three times.

iv) No. of zeroes =2 as graph intersect x-axis two times

v) No. of zeroes =4 as graph intersect x-axis four times

vi) No. of zeroes =0 as graph doesn’t intersect at x-axis

Exercise 2.2

1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. 

(i) x² – 2x – 8 (ii) 4s² – 4s + 1 (iii) 6x² – 3 – 7x (iv) 4u² + 8u (v) t ² – 15 (vi) 3x² – x – 4

(i) x² – 2x – 8 

Let

x²-2x-8=0

x²-4x+2x-8=0

x(x-4)+2(x-4)=0

(x-4)(x+2)=0

x=4,-2

General equation can be represented as:

ax² + bx + c = 0

x² - 2x - 8 = 0

a = 1, b = -2, c = -8

Now, we will verify the roots

a + b = - b/a

4 - 2 = - (-2)/1

2 = 2

(ii) 4s² – 4s + 1

Let

4s² - 4s + 1 = 0

4s² - 2s - 2s + 1 = 0

2s (2s -1) -1(2s -1) = 0

(2s -1)(2s -1) = 0

s = 1/2 , 1/2

General equation can be represented as:

as² + bs + c = 0 4s² - 4s +1 = 0

a = 4, b = -4, c = 1

Now, we will verify the roots

α + β = - b/a

1/2  + 1/2 = - (-4)/4

1=1

(iii) 6x² - 3 - 7x

On rearanging the equation: 6x² - 7x - 3

Let

6x² - 7x - 3 = 0

6x² - 9x + 2x - 3 = 0

3x (2x - 3) +1(2x - 3) = 0

(3x +1)(2x - 3) = 0

x = -1/3, 3/2

General equation can be represented as:

ax² + bx + c = 0 6x² - 7x - 3 = 0

a = 6, b = -7, c = -3

Now, we will verify the roots

α + β = - b/a

-1/3 + 3/2= - (-7)/6

-2+9/6 = 7/6

7/6 =7/6

(iv) 4u² + 8u

Let

4u² + 8u = 0

4u (u + 2) = 0

u = 0, -2

General equation can be represented as:

au² + bu + c = 0 4u² + 8u = 0

a = 4, b = 8, c = 0 

Now, we will verify the roots

α + β = - b/a

0-2= -(8)/4

-2=-2

(v) t ² - 15

Let

t ² - 15 = 0

t ² = 15

t =± √15

General equation can be represented as:

at ² + bt + c = 0

t² -15 = 0

a = 1, b = 0, c = -15

Now, we will verify the roots

α + β = - b/a

√15 - √15 =- 0/1

0=0

(vi) 3x² - x - 4

 Let

3x² - x - 4 = 0

3x² - 4x + 3x - 4 = 0

x (3x - 4) + 1(3x - 4) = 0

(3x - 4)( x + 1) = 0

x = -1, 4/3

General equation can be represented as:

ax² + bx + c = 0 3x² - x - 4 = 0

a = 3, b = -1, c = -4

Now, we will verify the roots

α + β = - b/a

-1 + 4/3+ - (-1)/3

-3+4/3 = 1/3

1/3= 1/3

2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively

(i) 1/4 , 1 ii) √2 , 1/3  iii) 0, √5 , iv) 1, 1 v) -1/4 ,1/4  vi) 4,1

(i) 1/4 , 1

Let α + β are the zeroes of a quadratic polynomial 

Now, We have,

α + β = 1/4, αβ = -1

α + β = 1/4

-b/a= 1/4

b/a = -1/4

αβ = -1

c/a = -1

c/a = -4/4

Thus,

a = -4, b = 1, c = 4

Equation is:

-4x² + x + 4 = 0

4x² - x - 4 = 0

 ii) √2 , 1/3

Let α + β are the zeroes of a quadratic polynomial 

Now, We have,

α + β = √2, αβ = 1/3

α + β = √2

b/a = √2

b/a = -3 √2 /3

αβ = 1/3

c/a = 1/3 

Thus,

a = 3,b = -3√2, c = 1 

Equation is

3x² - 3 √2 +1 = 0

 iii) 0, √5

Let α + β are the zeroes of a quadratic polynomial 

Now, We have,

α + β = 0, αβ = √5

α + β = 0

-b/a  = 0

-b/a = 0/1

αβ = √5

c/a = √5/1

Thus, 

a= 1, b=0, c= √5

Equation is, 

x² + 0x + √5 = 0

x² + √5 = 0

iv) 1, 1

Let α + β are the zeroes of a quadratic polynomial 

Now, We have,

α + β = 1, αβ = 1

α + β = 1

-b/a = 1

b/a = -1/1

αβ = 1

c/a = 1/1

Thus, 

a=1, b= -1, c=1

Equation is

x² - x +1 = 0

v) -1/4 ,1/4  

Let α + β are the zeroes of a quadratic polynomial 

Now, We have,

α + β = -1/4 , αβ = 1/4

α + β = -1/4

-b/a = -1/4

b/a = 1/4

αβ = 1/4

c/a = 1/4

Thus,

a = 4,b = 1, c = 1 

Equation is

4x² + x + 1 = 0

vi) 4,1

Let α + β are the zeroes of a quadratic polynomial 

Now, We have,

α + β = 4 , αβ = 1

α + β = 4

-b/a = 4

b/a = -4/1 

αβ = 1

c/a = 1/1 

Thus,

a = 1,b = -4, c = 1

Equation is

x² - 4x +1 = 0

For all the questions given in CBSE Class 10 Mathematics NCERT book, you will find detailed and accurate answers at Jagran Josh. These solutions will help you find the right approach to solve different questions accurately and secure high marks in exams.

Check NCERT Solutions for Class 10 Maths chapter 2 Polynomials (PDF)

You are suggested to follow the latest NCERT Class 10 Maths Book to study the topics that have been prescribed for the current academic session. Some of the topics as well as a few chapters have been removed from the book. So, keep the latest edition of the book with you to avoid wasting time on topics which are no more a part of the latest syllabus.

Check:

• NCERT Books for Class 10 - All Subjects

• NCERT Solutions for Class 10 - All Subjects