CBSE Class 12 Maths Chapter 6 Application of Derivatives Revision Notes Download PDF

CBSE Class 12 Mathematics Chapter 6 Application of Derivatives Revision Notes: With the 2023 board exams around the corner, it's time to put down the books and begin revising the topics. Mathematics is a subject that requires constant practice and thorough revision. In the final stage of the session year, it’s advised to students to focus on revision rather than picking new concepts to learn.

The CBSE Class 12 board exams are set to start from February 15, 2024, and the mathematics paper will be held on March 9. The sixth chapter in the Class 12 math books is Application of Derivatives. It’s one of the most important and longest chapters in the curriculum and holds considerable importance in the final exam. One long-answer question is usually asked from the Application of Derivatives.

You can check out the CBSE Class 12 Chapter 6 Application of Derivatives revision notes here, along with supporting study material like mind maps and multiple choice questions.

CBSE Class 12 Maths Chapter 6 Application of Derivatives Revision Notes

Basic Definitions and Summary:

Rate of Change of Quantities

Increasing & Decreasing Function

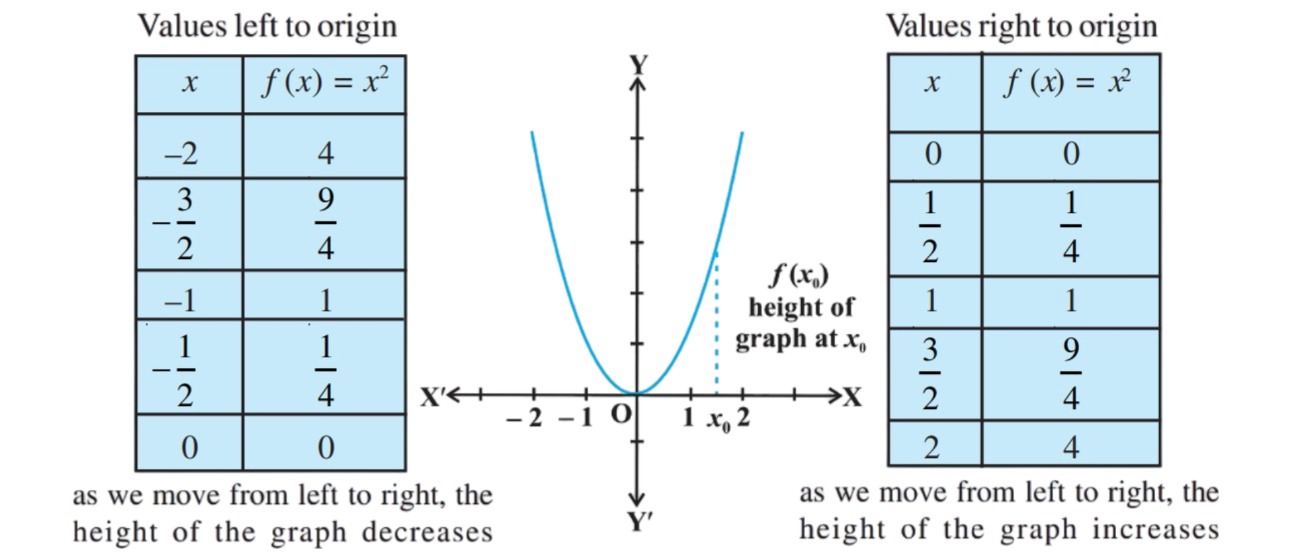
A function ƒ is said to be

(a) increasing on an interval (a, b) if

x₁ < x₂ in (a, b) ⇒ ƒ (x₁ ) ≤ ƒ(x₂) ƒor all x₁ , x₂ ∈ (a, b).

Alternatively, if ƒ’(x) ≥ 0 for each x in (a, b)

(b) decreasing on (a,b) if

x₁ < x₂ in (a, b) ⇒ ƒ (x₁) ≥ ƒ (x₂) for all x₁ , x₂ ∈ (a, b).

Alternatively, if ƒ ′(x) ≤ 0 for each x in (a, b)

Maxima & Minima

First Derivative Test

Let ƒ be a function defined on an open interval I and Let f be continuous at a critical point c in I. Then,

(i) If ƒ ′(x) changes sign from positive to negative as x increases through c, i.e., if ƒ ′(x) > 0 at every point sufficiently close to and to the left of c, and ƒ ′(x) < 0 at every point sufficiently close to and to the right of c, then c is a point of local maxima.

(ii) If ƒ ′(x) changes sign from negative to positive as x increases through c, i.e., if ƒ ′(x) < 0 at every point sufficiently close to and to the left of c, and ƒ ′(x) > 0 at every point sufficiently close to and to the right of c, then c is a point of local minima.

(iii) If ƒ ′(x) does not change sign as x increases through c, then c is neither a point of local maxima nor a point of local minima. In fact, such a point is called the point of inflexion.

Second Derivative Test

Let ƒ be a function defined on an interval I and c ∈ I. Let ƒ be twice differentiable at c. Then,

(i) x = c is a point of local maxima if ƒ ′(c) = 0 and ƒ ″(c) < 0

The values ƒ (c) is local maximum value of ƒ .

(ii) x = c is a point of local minima if ƒ ′(c) = 0 and ƒ ″(c) > 0

In this case, ƒ (c) is local minimum value of ƒ .

(iii) The test fails if ƒ ′(c) = 0 and ƒ ″(c) = 0.

In this case, we go back to the first derivative test and find whether c is a point of maxima, minima or a point of inflexion.

Working rule for finding absolute maxima and/or absolute minima

Step 1: Find all critical points of ƒ in the interval, i.e., find points x where either ƒ ′(x) = 0 or ƒ is not differentiable.

Step 2: Take the end points of the interval.

Step 3: At all these points (listed in Step 1 and 2), calculate the values of ƒ.

Step 4: Identify the maximum and minimum values of ƒ out of the values calculated in Step 3. This maximum value will be the absolute maximum value of ƒ and the minimum value will be the absolute minimum value of f.

With the exams approaching fast, the above revision notes for mathematics class 12 chapter 6 application of derivatives will come in handy for students looking to achieve top marks. Thoroughly studying the revision notes will help you boost your exam preparation. In the meantime, do check out the following study resources like NCERT book solutions, MCQs and mind maps of Application of Derivatives.

Recommended: