CBSE Class 12 Maths MCQs: The CBSE Class 12 Maths Board Exam 2025, scheduled for March 08, 2025, requires dedicated practice, especially with Multiple-Choice Questions (MCQs), which are crucial for scoring well. To help students prepare effectively, we have compiled 50 important MCQs from previous years' papers and CBSE sample papers. These carefully selected questions cover key concepts from all chapters, ensuring a comprehensive revision before the exam.
Solving these high-weightage MCQs will help students strengthen their understanding, improve accuracy, and boost confidence for the final exam. Regular practice of these MCQs will enhance problem-solving skills and increase the chances of securing better marks in the CBSE Class 12 Maths exam on March 08, 2025.
Also Check:
CBSE Class 12th Maths Paper: Key Highlights
Particulars | Details |
| Exam Conducting Body | Central Board of Secondary Education (CBSE) |
| Subject | Maths |
| Mode of Exam | Offline |
| Exam Duration | 3 Hours |
| Medium of Exam | English / Hindi |
| Type of Questions | MCQs, Short and Long Answer Type Questions |
| Theory Marks | 80 |
| Internal Assessment | 20 |
| Total Marks | 100 |
| Passing Marks | 33% in aggregate |
CBSE Class 12th Maths Exam Top 50 MCQs
Here are 50 important multiple-choice questions (MCQs) from all chapters in your 12th Maths syllabus along with their answers:
1.Let A = {1, 2, 3} and consider the relation R = {1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1,3)}. Then R is
(a) reflexive but not symmetric
(b) reflexive but not transitive
(c) symmetric and transitive
(d) neither symmetric, nor transitive
2. The function f : R → R defined by f(x) = 3 – 4x is
(a) Onto
(b) Not onto
(c) None one-one
(d) None of these
3. How many distinct relations can be defined on the set A = {1,2,3}?
(a) 29
(b) 23
(c) 9
(d) 26
4. If f: R → R be given by f(x) = (3 – x3)1/3, then fof(x) is
(a) x1/3
(b) x3
(c) x
(d) (3 – x3)
5. Which of the following is the principal value of sin-1(1)?
a) π/2
b) π/4
c) π
c) 0
6. The domain of the function f(x) = sin-1(x) is:
a) [-1, 1]
b) (-∞, ∞)
c) [0, 1]
c) [0, π/2]
7. The value of tan-1(√3) is:
a) π/4
b) π/3
c) π/6
c) 2π/3
8. The value of sin(cos-1(1/2)) is:
a) √3/2
b) 1/√3
c) 2/√3
c) 1/2
9. Matrices A and B will be inverse of each other only if:
(a) AB = BA
(b) AB-BA = 0
(c) AB = 0, BA = I
(d) AB = BA = I
10. If A and B are two matrices of the order 3 × m and 3 × n, respectively, and m = n, then the order of matrix (5A – 2B) is
(a) m x 3
(b) 3 x 3
(c) m x n
(d) 3 x n
11. Which of the following is correct?
(a) Determinant is a square matrix.
(b) Determinant is a number associated with a matrix.
(c) Determinant is a number associated with a square matrix.
(d) None of these
12. If A is an invertible matrix of order 2, then det (A–1) is equal to
(a) det (A)
(b) 1/det (A)
(c) 1
(d) 0
13. The function f(x) = [ln(1+ax)-ln(1-bx)]/x, not defined at x=0. The value should be assigned to f at x=0, so that it is continuous at x =0, is
(a) a+b
(b) a-b
(c) b-a
(d) ln a+ ln b
14. If x sin(a+y) = sin y, then dy/dx is equal to
(a) [sin2(a+y)]/sin a
(b) sin a /[sin2(a+y)]
(c) [sin(a+y)]/sin a
(d) sin a /[sin(a+y)]
14. The value of c in Rolle’s theorem for the function, f(x) = sin 2x in [0, π/2] is
(a) π/4
(b) π/6
(c) π/2
(d) π/3
15. If f(x) = 3x4 - 4x2 + 5, then the interval for which f(x) satisfy all the conditions of Rolle’s theorem, is
(a) (0, 2)
(b) (-1, 1)
(c) (-1, 0)
(d) (-1, 2)
16. The function f(x) = x5 – 5x4 + 5x3 – 1 has
(a) one minima and two maxima
(b) two minima and one maxima
(c) two minima and two maxima
(d) one minima and one maxima
17. If x increases at the rate of 2 m/sec at the instant when x = 3 m, y = 1 m, at what rate must y be changing in order that the function 2xy - 3x2y shall be neither increasing nor decreasing?
(a) 32/21 m/sec; increasing
(b) 32/21 m/sec; decreasing
(c) 8/21 m/sec; increasing
(d) 8/21 m/sec; decreasing
18. ∫ 2x dx = f(x) + C, then f(x) is
(a) 2x
(b) 2xloge2
(c) 2x/loge2
(d) 2x+1/x+1
19. f a is such that 0∫a x d x ≤ a + 4, then
(a) 0 ≤ a ≤ 4
(b) -2 ≤ a ≤ 0
(c) a ≤ -2 or a ≤ 4
(d) -2 ≤ a ≤ 4
20. If ∫dx/[(x+2)(x2+1)] = a log |1 + x2| + b tan–1x + (1/5) log |x + 2| + C, then
(a) a = -1/10, b = -2/5
(b) a = 1/10, b = -2/5
(c) a = -1/10, b = 2/5
(d) a = 1/10, b = 2/5
21. The area of the region bounded by the curve x² = 4y and the straight line x = 4y – 2 is
(a) 3/8 sq. units
(b) 5/8 sq. units
(c) 7/8 sq. units
(d) 9/8 sq. units
22. The area of the region bounded by the curve y = √16-x2 and x-axis is
(a) 8π sq. units
(b) 20π sq. units
(c) 16π sq. units
(d) 256 sq. units
23. The area bounded by the lines y = |x| - 1 and y = -|x| + 1 is
(a) 1 sq. unit
(b) 2 sq. unit
(c) 2√2 sq. unit
(d) 4 sq. unit
24. The area bounded by the curves y=cosx, y=sinx, Y-axis and 0⩽x ⩽π/4 is _____ .
(a) 2(√2-1)
(b) √2-1
(c) √2+1
(d) √2
25. Solution of differential equation xdy – ydx = Q represents
(a) a rectangular hyperbola
(b) parabola whose vertex is at origin
(c) straight line passing through origin
(d) a circle whose centre is at origin
26. What is the degree of differential equation (y’’’)2 + (y’’)3 + (y’)4 + y5 = 0?
(a) 2
(b) 3
(c) 4
(d) 5
27. The solution of (x+ logy)dy +ydx =0 where y(0) =1 is
(a) y(x−(A)) + ylogy = 0
(b) y(x−1+logy) + 1 = 0
(c) xy+ ylogy +1 = 0
(d) None of these
28. What is the differential equation of the family of circles touching the y-axis at the origin?
(a) 2xyy’ + x2 = y2
(b) 2xyy’’ + x’ = y2
(c) 2xyy’ – x2 = y2
(d) xyy’ + x2 = y2
29. The scalar product of 5i + j – 3k and 3i – 4j + 7k is:
(a) 15
(b) -15
(c) 10
(d) -10
30. The magnitude of the vector 6i + 2j + 3k is equal to:
(a) 5
(b) 1
(c) 7
(d) 12
30. If vectors |A.B|=|A×B|, then angle between A and B is
(a) 60o
(b) 30o
(c) 90o
(d) 45o
31. 
32. 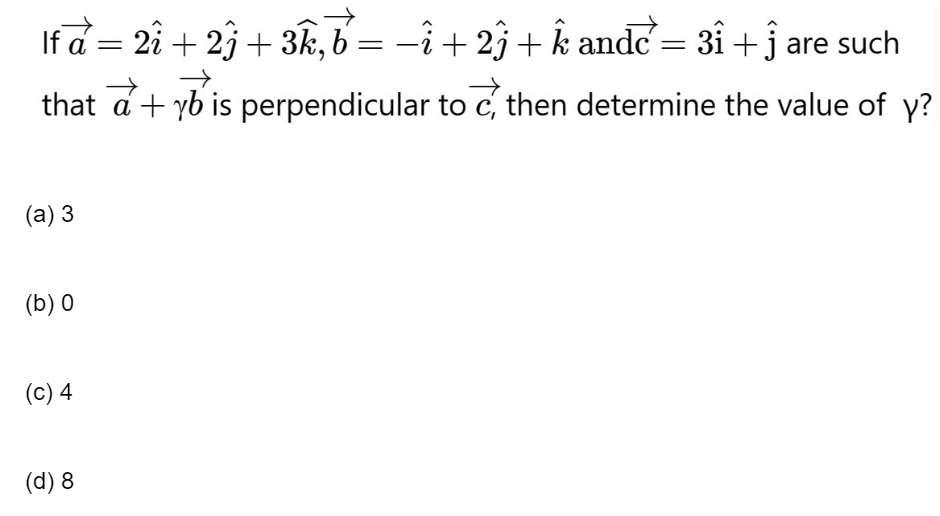
33. If the direction cosines of a line are k/3,k/3,k/3, then value of k is
(a) k > 0
(b) 0 < k < 1.
(c) k = 1/3
(d) k = ±3
34. Find the equation of the plane passing through the points P(1, 1, 1), Q(3, -1, 2), R(-3, 5, -4).
(a) x + 2y = 0
(b) x – y – 2 = 0
(c) -x + 2y – 2 = 0
(d) x + y – 2 = 0
35. The vector equation for the line passing through the points (–1, 0, 2) and (3, 4, 6) is:
(a) i +2k + λ(4i + 4j + 4k)
(b) i –2k + λ(4i + 4j + 4k)
(c) -i+2k+ λ(4i + 4j + 4k)
(d) -i+2k+ λ(4i – 4j – 4k)
36. If l, m, n are the direction cosines of a line, then;
(a) l2+ m2+ 2n2 = 1
(b) l2+ 2m2+ n2 = 1
(c) 2l2+ m2+ n2 = 1
(d) l2+ m2+ n2 = 1
37. If a line has direction ratios 2, – 1, – 2, determine its direction cosines:
(a) ⅓, ⅔, -⅓
(b) ⅔, -⅓, -⅔
(c) -⅔, ⅓, ⅔
(d) None of the above
38. Maximize Z = 3x + 5y, subject to constraints: x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0
(a) 20 at (1, 0)
(b) 30 at (0, 6)
(c) 37 at (4, 5)
(d) 33 at (6, 3)
39. Minimize Z = 20x1 + 9x2, subject to x1 ≥ 0, x2 ≥ 0, 2x1 + 2x2 ≥ 36, 6x1 + x2 ≥ 60.
(a) 360 at (18, 0)
(b) 336 at (6, 4)
(c) 540 at (0, 60)
(d) 0 at (0, 0)
40. In solving the LPP: minimize f = 6x + 10y subject to constraints x ≥ 6, y ≥ 2, 2x + y ≥ 10, x ≥ 0, y ≥ 0 redundant constraints are
(a) x ≥ 6
(b) 2x + y ≥ 10, x ≥ 0, y ≥ 0
(c) x ≥ 6, y ≥ 2
(d) None of these
41. The maximum value of Z = 3x + 4y subjected to constraints x + y ≤ 40, x + 2y ≤ 60, x ≥ 0, y ≥ 0 is
(a) 130
(b) 120
(c) 150
(d) 140
42. Find P(E|F), where E: no tail appears, F: no head appears when two coins are tossed in the air.
(a) 0
(b) ½
(c) 1
(d) None of the above
43. If P(a) = 0,4, P(b) = 0.8 and P(B|A) = 0.6 then P(A∪B) is equal to
(a) 0.24
(b) 0.3
(c) 0.48
(d) 0.96
44. If A and B are two independent events, then the probability of occurrence of at least one of A and B is given by:
(a) 1+ P(A′) P (B′)
(b) 1− P(A′) P (B′)
(c) 1− P(A′) + P (B′)
(d) 1− P(A′) – P (B′)
45. If P(A ∩ B) = 70% and P(B) = 85%, then P(A/B) is equal to:
(a) 17/14
(b) 14/17
(c) ⅞
(d) ⅛
46. A person writes 4 letters and addresses 4 envelopes. If the letters are placed in the envelopes at random, then the probability that all letters are not placed in the right envelopes, is
(a) 23/24
(b) 15/24
(c) 11/24
(d) 1/4
47. If E and F are independent events, then;
(a) P(E ∩ F) = P(E)/ P(F)
(b) P(E ∩ F) = P(E) + P(F)
(c) P(E ∩ F) = P(E) . P(F)
(d) None of the above
48. A police officer fires three bullets at a thief. The probability that the thief will be killed by one bullet is 0.8. Find the probability of the thief being still alive?
(a) 0.008
(b) 0.0016
(c) 0.64
(d) None of the above
49. The mean and the variance of a binomial distribution are 4 and 2 respectively. Then the probability of 2 success is
(a) 28/256
(b) 219/256
(c) 128/256
(d) 37/256
50. The probability of a student getting 1, 2, 3 division in an examination are 1/10, 3/5 and 1/4 respectively. The probability that the student fails in the examination is
(a) 27/100
(b) 83/100
(c) none of these
(d) 197/200
CBSE Class 12th Maths Exam Top 50 MCQs Solutions
Check out the answers below for all the MCQs questions provided above:
Q. No. | Answer |
|---|---|
| 1 | (b) Reflexive but not transitive |
| 2 | (a) Onto |
| 3 | (a) 2⁹ = 512 |
| 4 | (c) x |
| 5 | (a) π/2 |
| 6 | (a) [-1, 1] |
| 7 | (b) π/3 |
| 8 | (d) 1/2 |
| 9 | (d) AB = BA = I |
| 10 | (d) 3 × n |
| 11 | (c) Determinant is a number associated with a square matrix |
| 12 | (b) 1/det(A) |
| 13 | (b) a - b |
| 14 | (b) sin a / sin²(a + y) |
| 15 | (a) π/4 |
| 16 | (b) (-1,1) |
| 17 | (a) One minima and two maxima |
| 18 | (b) 32/21 m/sec; decreasing |
| 19 | (c) 2x / logₑ2 |
| 20 | (d) -2 ≤ a ≤ 4 |
| 21 | (c) a = -1/10, b = 2/5 |
| 22 | (c) 16π sq. units |
| 23 | (b) 2 sq. unit |
| 24 | (b) √2 - 1 |
| 25 | (c) Straight line passing through origin |
| 26 | (c) 4 |
| 27 | (c) xy + y log y + 1 = 0 |
| 28 | (c) 2xyy' - x² = y² |
| 29 | (b) -15 |
| 30 | (c) 7 |
| 31 | (c) 90° |
| 32 | To be Given |
| 33 | (d) k = ±3 |
| 34 | (c) -x + 2y - 2 = 0 |
| 35 | (c) -i + 2k + λ(4i + 4j + 4k) |
| 36 | (d) l² + m² + n² = 1 |
| 37 | (b) ⅔, -⅓, -⅔ |
| 38 | (c) 37 at (4,5) |
| 39 | (b) 336 at (6,4) |
| 40 | (c) x ≥ 6, y ≥ 2 |
| 41 | (b) 120 |
| 42 | (a) 0 |
| 43 | (d) 0.96 |
| 44 | (b) 1 - P(A') P(B') |
| 45 | (b) 14/17 |
| 46 | (a) 23/24 |
| 47 | (c) P(E ∩ F) = P(E) * P(F) |
| 48 | (b) 0.0016 |
| 49 | (a) 28/256 |
| 50 | (a) 27/100 |
Comments
All Comments (0)
Join the conversation