CBSE Class 12 Maths Repeated Questions: The CBSE Class 12 Mathematics Board Exam 2025 is set to be conducted on March 8, 2025. As the exam day approaches, practicing frequently asked questions from previous years can significantly boost your preparation. Here, we have compiled the most repeated questions that are commonly seen in CBSE board exams. These questions are curated according to the latest CBSE exam pattern 2024-25, covering 1-mark, 3-mark, and 4-mark questions to help students score better.
Mathematics requires precision, strong conceptual understanding, and quick calculations. Memorizing important formulas and practising these repeated questions will enhance your speed and accuracy, making it easier to secure higher marks. For the complete set of important questions, read the full article below.
Also Check: CBSE Class 12 Maths Top 50 MCQs for Board Exam 2025
Most Repeated Questions in Maths Class 12 CBSE Board: Chapter-Wise
Here you will find the most important question for CBSE Class 12 mathematics that you must practice. The questions in the CBSE Class 12 Maths Exam 2025 will be based on these. These are the types of questions that will be asked in the CBSE Class 12 Maths exam 2025.
1. Relations and Functions
Q1. If R = {(a, a3): a is a prime number less than 5} be a relation. Find the range of R .
Q2. If f: {1,3, 4} → {1, 2, 5} and g: {1,2, 5} → {1, 3} given by f = {(1,2), (3, 5), (4,1)} and g = {(1,3), (2, 3), (5,1)}. Write down gof.
Q3. Let R is the equivalence relation in the set A = {0,1, 2, 3, 4, 5} given by R = {(a, b) : 2 divides (a – b)}. Write the equivalence class [0].
Q4. If R = {(x, y): x + 2y = 8} is a relation on N, then write the range of R.
Q5. If A = {1, 2, 3}, S = {4, 5,6, 7} and f = {(1, 4), (2, 5), (3, 6)} is a function from A to B. State whether f is one-one or not.
Q6. If f : R → R is defined by f{x) = 3x + 2, then define f[f(x)].
Q7. Write fog, if f: R → R and g:R → R are given by f(x) = |x| and g(x) = |5x – 2|.
Q8. Write fog, if f: R → R and g:R → R are given by f(x) = 8x3 and g(x) = xy3.
Q9. State the reason for the relation R in the set {1, 2, 3} given by R = {(1, 2), (2,1)} not to be transitive.
Q10. What is the range of the function?
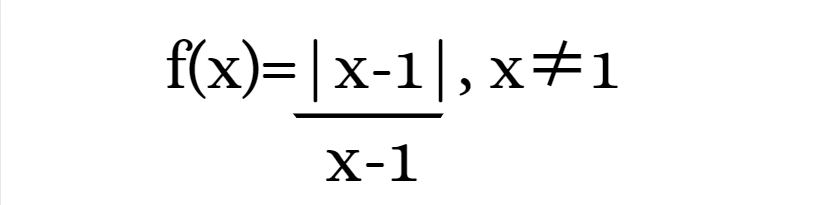
2. Inverse Trigonometric Functions
Q1. Write the value of
tan-1 (√3) – cot-1 (- √3).
Q2. Find the principal value of
tan-1√3 – sec-1 (- 2).
Q3. ![]()
Q4. Write the principal value of cos-1 [cos(680)°].
Q5. Write the value of cos-1 (1/2) – 2 sin-1 (1/2)
Q6. Using the principal values, write the value of cos-1(1/2) + 2 sin-1(1/2).
Q7. What is the principal value of tan-1 (- 1)?
Q8. Write the principal value of sin-1(−1/2).
3. Matrices
Q1. Write the number of all possible matrices of order 2 × 2 with each entry 1, 2 or 3.
Q2. Write the element a of a 3 × 3 matrix A = [aij], whose elements are given by aij = |i−j|/2
Q3. If A is a square matrix such that A2 = A, then write the value of 7A — (I + A)3, where I is an identity matrix.
Q4. 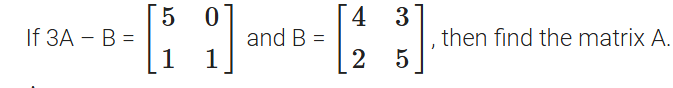
Q5. If a matrix has 5 elements, then write all possible orders it can have.
Q6. 
4. Determinants
Q1.
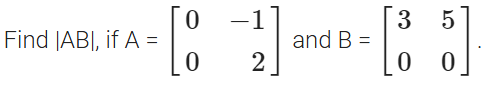
Q2.

Q3.
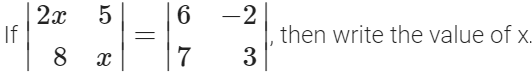
5. Continuity and Differentiability
Q1.
Q2.
6. Application of Derivatives
Q1. The total cost C(x) associated with the production of x units of an item is given by C(x) = 0.005x3 – 0.02x2 + 30x + 5000. Find the marginal cost when 3 units are produced, where by marginal cost we mean the instantaneous rate of change of total cost at any level of output.
Q2. Show that the function f(x) = x3 – 3x2 + 6x – 100 is increasing on R.
Q3. Show that the function f(x) = 4x3 – 18x2 + 27x – 7 is always increasing on R.
Q4. The volume of a cube is increasing at the rate of 8 cm3/s. How fast is the surface area increasing when the length of its edge is 12 cm?
Q5. The length x of a rectangle is decreasing at the rate of 5 cm/min and the width y is increasing at the rate of 4 cm/min. When x = 8 cm and y = 6 cm, find the rate of change of
(i) the perimeter.
(ii) area of rectangle.
7. Integrals
Q1. 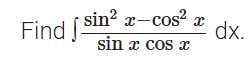
Q2. 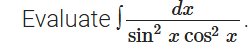
Q3. ![]()
Q4. 
8. Application of Integrals
Q1. Using integration, find the area of triangle whose vertices are (2, 3), (3, 5) and (4, 4).
Q2. Using integration, prove that the curves y2 = 4x and x2 = 4y divide the area of the square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.
Q3. Using integration, find the area of the triangular region whose sides have the equations y = 2x + 1, y = 3x + 1 and x = 4.
Q4. Using integration, find the area of region bounded by the triangle whose vertices are (- 2, 1), (0, 4) and (2, 3).
Q5. Using integration, find the area of the region bounded by the curves y = √4−x2, x2 + y2 – 4x = 0 and the x-axis.
Q6. Using integration, find the area of the region in the first quadrant enclosed by the Y-axis, the line y = x and the circle x2 + y2 = 32.
Q7. Using integration, find the area of the region bounded by the line x – y + 2 = 0, the curve x = √y and Y-axis.
Q8. Using integration, find the area of the region bounded by the curves y = |x + 1| + 1, x = – 3, x = 3 and y = 0.
Q9. Using integration, find the area of the region bounded by the triangle whose vertices are (- 1, 2), (1, 5) and (3, 4).
Q10. Find the area of the region bounded by the parabola y = x2 and the line y = |x|.
9. Differential Equations
Q1. Find the differential equation representing the family of curves y = ae2x + 5 constant.
Q2. Find the differential equation representing the family of curves V = A/r + B, where A and B are arbitrary constants.
Q3. Write the differential equation obtained by eliminating the arbitrary constant C in the equation representing the family of curves xy = C cos x.
Q4. Write the differential equation representing the family of curves y = mx, where m is an arbitrary constant.
Q5. Find the differential equation of the family of curves y = Ae2x + Be-2x, where A and B are arbitrary constants.
Q6. Form the differential equation of the family of parabolas having vertex at origin and axis along positive Y-axis.
Q7. Find the differential equation of family of circles touching Y-axis at the origin.
Q8. Write the solution of the differential equation dy/dx = 2-y
10. Vector Algebra
Q1. Find the unit vector in the direction of the sum of the vectors 2î + 3ĵ – k̂ and 4î – 3ĵ + 2k̂.
Q2. Find a vector in the direction of vector 2î – 3ĵ + 6k̂ which has magnitude 21 units.
Q3. Find a vector a of magnitude 5√2, making an angle of π4 with X-axis, π2 with Y-axis and an acute angle 0 with Z-axis.
Q4. Find the angle between X-axis and the vector î + ĵ + k̂.
Q5. ![]()
Q6. Write the direction cosines of vector -2î + ĵ – 5k̂.
Q7. What is the cosine of angle which the vector √2î + ĵ + k̂ makes with Y-axis?
Q8. Find the area of a parallelogram whose adjacent sides are represented by the vectors 2 î – 3 k̂ and 4 ĵ + 2 k̂.
11. Three Dimensional Geometry
Q1. If a line makes angles 90°, 135°, 45° with the x, y and z axes respectively, find its direction cosines.
Q2. What are the direction cosines of a line which makes equal angles with the coordinate axes?
Q3. If a line makes angles 90°, 60° and θ with X, Y and Z-axis respectively, where θ is acute angle, then find θ.
Q4. Write the distance of a point P(a, b, c) from X-axis.
Q5. Write the vector equation of a line passing through point (1, – 1, 2) and parallel to the line whose equation is x−3/1=y−1/2=z+1/−2.
Q6. Find the vector equation of the line passing through the point A (1, 2, – 1) and parallel to the line 5x – 25 = 14 – 7y = 35 z.
Q7. The x-coordinate of a point on the line joining the points P(2, 2, 1) and Q(5, 1, – 2) is 4. Find its z-coordinate.
12. Linear Programming
Q1. Two tailors A and B, earn ₹ 300 and ₹ 400 per day respectively. A can stitch 6 shirts and 4 pairs of trousers while B can stitch 10 shirts and 4 pairs of trousers per day. To find how many days should each of them work and if it is desired to produce at least 60 shirts and 32 pairs of trousers at a minimum labour cost, formulate this as an LPP.
Q2. Maximise and minimise Z = x + 2y subject to the constraints
x + 2 y ≥ 100
2x – y ≤ 0
2x+ y ≤ 200
x, y ≥ 0
Solve the above LPP graphically.
Q3. A company produces two types of goods, A and B, that require gold and silver. Each unit of type A requires 3 g of silver and 1 g of gold while that of type B requires 1 g of silver and 2 g of gold. The company can use at the most 9 g of silver and 8 g of gold. If each unit of type A brings a profit of ₹ 40 and that of type B ₹ 50, find the number of units of each type that the company should produce to maximize profit. Formulate the above LPP and solve it graphically and also find the maximum profit.
Q4. A retired person wants to invest an amount of ₹ 50000. His broker recommends investing in two types of bonds A’ and ‘B’ yielding 10% and 9% return respectively on the invested amount. He decides to invest at least ₹ 20000 in bond A’ and at least ₹ 10000 in bond ‘B’. He also wants to invest at least as much in bond A’ as in bond ‘B’. Solve this linear programming problem graphically to maximise his returns.
Q5. Find graphically, the maximum value of Z = 2x + 5y, subject to constraints given below
2x+ 4y ≤ 8; 3x + y ≤ 6
x + y ≤ A; x ≥ 0, y ≥ 0.
13. Probability
Q1. If P(not A) = 0.7, P(B) = 0.7 and P(B/A) = 0.5, then find P(A/B).
Q2. A and B throw a pair of dice alternately, till one of them gets a total of 10 and wins the game. Find their respective probabilities of winning, if A starts first.
Q3. Two groups are competing for the positions of the Board of Directors of a corporation. The probabilities that the first and second groups will win are 0.6 and 0.4 respectively. Further, if the first group wins, the probability of introducing a new product is 0.7 and the corresponding probability is 0.3 if the second group wins. Find the probability that the new product introduced way by the second group.
Q4. A bag A contains 4 black and 6 red balls and bag B contains 7 black and 3 red balls. A die is thrown. If 1 or 2 appears on it, then bag A is chosen, otherwise bag B. If two balls are drawn at random (without replacement) from the selected bag, find the probability of one of them being red and another black.
Q5. From a lot of 15 bulbs which include 5 defectives, a sample of 2 bulbs is drawn at random (without replacement). Find the probability distribution of the number of defective bulbs.
Q6. Find the mean number of heads in three tosses of a coin.
Q7.Find the probability distribution of number of doublets in three tosses of a pair of dice.
Q8. A bag contains 3 red and 7 black balls. Two balls are selected at random one by one without replacement. If the second selected ball happens to be red, what is the probability that the first selected ball is also red?
Q9. Three cards are drawn at random (without replacement) from a well-shuffled pack of 52 playing cards. Find the probability distribution of number of red cards. Hence, find the mean of the distribution.
Q10. Two numbers are selected at random (without replacement) from positive integers 2, 3, 4, 5, 6 and 7. Let X denote the larger of the two numbers obtained. Find the mean and variance of the probability distribution of X.
CBSE Class 12 Maths Syllabus (2024-25)
Get the detailed syllabus for class 12 Maths, outlining all the topics and units you need to cover for your board exams. Stay on track with a clear understanding of the subjects and their weightage.
CBSE Class 12 Deleted Syllabus 2025
Check ot the link for the topics that have been updated and deleted from the latest syllabus of CBSE for the academic year 2024-25.
CBSE Maths Topper Answer Sheet Class 12 For 2025 Board Exams
These answer sheets are provided for students of the latest academic batch to go through and understand how and where to write the answer. Check out the link below for more details:
CBSE Class 12 Maths 3 Month Study Plan 2025
Check 90 Days Study Plan to to prepare in an effective and well-organised manner for the CBSE Class 12 Maths Exam 2025. Check out the below mentioned link for detailed study plan for maths:
CBSE Class 12 Maths MCQs 2024-25
Prepare for your class 12 Maths exam with multiple-choice questions (MCQs) covering key chapters. These questions help in assessing your understanding of various topics and improve quick decision-making skills.
Most Repeated Questions for Class 12
Check out the below table for Most Repeated Questions for other subjects in class 12:
| CBSE Class 12 Physics Most Repeated Questions | CBSE Class 12 Chemistry Most Repeated Questions |
| CBSE Class 12 Biology Most Repeated Questions | CBSE Class 12 Physical Education Most Repeated Questions |
Comments
All Comments (0)
Join the conversation