NCERT Solutions for Class 10 Maths Chapter 8: Solving questions given in NCERT textbooks is important for students in preparation for the examination. Questions given in the NCERT books are always considered important as not only do they help students to analyse their understanding of the concepts involved in a chapter but also in preparing for the examinations. Students should have access to the accurate NCERT solutions. We have provided detailed answers for all the exercise questions for NCERT Class 10 Maths Chapter 8 Introduction to Trigonometry in this article.
Jagran Josh provides students with precise and well-structured NCERT solutions. These are prepared by the subject matter experts. Students should solve as many questions as they can to strengthen their understanding and ability to answer questions.
Students should study from NCERT Books as they help gain an understanding of concepts and strengthen their basics. These books are recommended due to their explanation of even difficult topics in simple and clear language.
Download the NCERT Solutions for Class 10 Maths Chapter 8 from the direct link given in this article.
NCERT Class 10 Maths Chapter 8 Introduction to Trigonometry Solutions
Go through the questions and answers from Exercise 8.1, 8.2 and 8.3 from NCERT Class 10 Chapter 8 Introduction to Trigonometry.
EXERCISE 8.1
Q. In ABC, right-angled at B, AB = 24 cm, BC = 7 cm.
Determine : (i) sin A, cos A (ii) sin C, cos C
Sol. In triangle ΔABC with right angle at B,
∠B = 90°
Given: AB = 24 cm and BC = 7 cm
Using Pythagoras theorem,
AC²=AB²+BC²
AC²=(24)²+7²
AC²=(576+49)
AC²=625 cm²
AC=√625=25
(i) Sin A Cos A
Sin A=Opposite side/hypotenuse=BC/AC=7/25
Cos A= Adjacent side/hypotenuse=AB/AC=24/25
(ii) Sin C Cos C
Sin C= AB/AC=24/25
Cos C=BC/AC=7/25
Q. Find tan P – cot R.
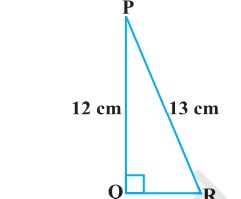
Sol. In triangle ΔPQR with right angle at Q,
Given,
PR = 13cm, PQ = 12cm
Using Pythagoras theorem,
PR²=QR²+PQ²
13²=QR²+12²
169=QR²+144
QR²=169-144
QR²=25
QR=√25=5
To find tan P – cot R:
tan (P) = Opposite side /Adjacent side = QR/PQ = 5/12
Cot (R) = Adjacent side/Opposite side = QR/PQ = 5/12
Therefore, tan (P) – cot (R) = 5/12 – 5/12 = 0
Therefore, tan(P) – cot(R) = 0
Q. If sin A = 3/4, calculate cos A and tan A.
Sol. Given a triangle ΔABC with right angle at B,
Given: Sin A = 3/4
Sin A = Opposite side /Hypotenuse= ¾
Let BC be 3k and AC will be 4k where k is a positive real number.
Using Pythagoras theorem,
AC²=AB²+BC²
(4k)²=AB²+(3k)²
16k²-9k²=AB²
AB=7k²
Therefore, AB = √7k
cos A=Adjacent side/Hypotenuse
AB/AC = √7k/4k = √7/4
Therefore, cos (A) = √7/4
tan(A) = Opposite side/Adjacent side
BC/AB = 3k/√7k = 3/√7
Therefore, tan A = 3/√7
Q. Given 15 cot A = 8, find sin A and sec A.
Sol. Given a triangle ΔABC with right angle at B,
Given: 15 cot A = 8
Cot A = 8/15
cot A = Adjacent side/Opposite side = AB/BC = 8/15
Let AB be 8k and BC will be 15k Where, k is a positive real number.
Using Pythagoras theorem,
AC²=AB²+BC²
AC²=(8k)²+(15k)2
AC²=64k²+225k²
AC²=289k²
Therefore, AC = 17k
sin A= Opposite side /Hypotenuse
Sin A = BC/AC = 15k/17k = 15/17
Therefore, sin A = 15/17
Sec (A) = Hypotenuse/Adjacent side
AC/AB = 17k/8k = 17/8
Therefore sec (A) = 17/8
Q. Given sec θ = 13/12, calculate all other trigonometric ratios.
Sol. Given a ΔABC with right angle at B,
sec θ =13/12 = Hypotenuse/Adjacent side = AC/AB
Let AC be 13k and AB will be 12k Where, k is a positive real number.
Using Pythagoras theorem,
AC²=AB²+BC²
(13k)²=(12k)²+BC²
169k²=144k²+BC²
BC²=169k²-144k²
BC²=25k²
Therefore, BC = 5k
Sin θ = Opposite Side/Hypotenuse = BC/AC = 5/13
Cos θ = Adjacent Side/Hypotenuse = AB/AC = 12/13
tan θ = Opposite Side/Adjacent Side = BC/AB = 5/12
Cosec θ = Hypotenuse/Opposite Side = AC/BC = 13/5
cot θ = Adjacent Side/Opposite Side = AB/BC = 12/5
Q. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Sol. Given ΔABC in which CD⊥AB
Cos (A) = cos (B)
AD/AC = BD/BC
AD/BD = AC/BC
Taking a constant value,
AD/BD = AC/BC = k
AD = k BD …(1)
AC = k BC …(2)
Using Pythagoras theorem,
CD²=BC²-BD²...(3)
CD²=AC²-AD²... (4)
AC²-AD²=BC²-BD²
K²(BC²-BD²)=(BC²-BD²) k²-1
AC=BC
∠A=∠B (Angles opposite to equal side are equal-isosceles triangle)
Q. If cot θ = 7/8, evaluate:
(i) (1 + sin θ)(1 – sin θ)/(1+cos θ)(1-cos θ)
(ii) cot2 θ
Sol. Given ΔABC in which ∠B = 90° and ∠C = θ
Given, cot θ = BC/AB = ⅞
Let BC = 7k and AB = 8k, where k is a positive real number
Using Pythagoras theorem,
AC²=AB²+BC²
AC²=(8k)²+(7k)²
AC²=64k²+49k²
AC²=113k²
AC=√113k
sin θ = AB/AC = Opposite Side/Hypotenuse = 8k/√113 k = 8/√113
cos θ = Adjacent Side/Hypotenuse = BC/AC = 7k/√113 k = 7/√113
(i) (1 + sin θ)(1 – sin θ)/(1+cos θ)(1-cos θ)=1-sin²θ/1-cos²θ
=1-(8/√113)²/1-(7/√113)²=49/64
(ii) cot²θ=(7/8)²=49/64
Q. If 3 cot A = 4, check whether (1-tan²A)/(1+tan² A) = cos² A – sin² A or not.
Sol. Given △ABC in which ∠B=90°
cot(A) = AB/BC = 4/3
Let AB = 4k an BC =3k, where k is a positive real number.
Using Pythagoras theorem,
AC²=AB²+BC²
AC²=(4k)²+(3k)²
AC²=16k²+9k²
AC²=25k²
AC=5k
tan(A) = BC/AB = 3/4
sin (A) = BC/AC = ⅗
cos (A) = AB/AC = 4/5
LHS=1-tan²A/1+tan²A=1-(3/4)²/1+(3/4)²=1-9/16/1+9/16=7/25
RHS=cos² A-sin² A=(4/5)²-(3/5)²=16/25-9/25=7/25
Since, R.H.S. =L.H.S.
Hence, (1-tan²A)/(1+tan² A) = cos² A – sin² A is proved.
Q. In triangle ABC, right-angled at B, if tan A =1/√3, find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Sol. Given ΔABC in which ∠B=90°
tan A = BC/AB = 1/√3
Let BC = 1k and AB = √3 k,
Where k is the positive real number of the problem
Using Pythagoras theorem,
AC²=AB²+BC²
AC²=(√3 k)²+(k)²
AC²=3k²+k²
AC²=4k²
AC = 2k
Sin A = BC/AC = ½
Cos A = AB/AC = √3/2
Sin C = AB/AC = √3/2
Cos C = BC/AC = ½
(i) sin A cos C + cos A sin C = (1/2) ×(1/2 )+ √3/2 ×√3/2 = 1/4 + 3/4 = 1
(ii) cos A cos C – sin A sin C = (√3/2 )(1/2) – (1/2) (√3/2 ) = 0
Q. In ∆PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Sol. Given that, PR + QR = 25 , PQ = 5
Let PR be x. ∴ QR = 25 - x
Using Pythagoras theorem,
PR² = PQ² + QR²
(25- x)²= 5²+ x²
25² + x² – 50x = 25 + x²
625 + x² -50x -25 – x²= 0
-50x = -600
x= -600/-50
x = 12 = QR
PR = 25- QR
PR = 25-12
PR = 13
(i) sin p = Opposite Side/Hypotenuse = QR/PR = 12/13
(ii) Cos p = Adjacent Side/Hypotenuse = PQ/PR = 5/13
(iii) tan p =Opposite Side/Adjacent side = QR/PQ = 12/5
Q. State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A =12/15 for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ =4/3 for some angle θ.
Sol. (i) False
ΔMNC in which ∠N = 90º,
MN = 3, NC = 4 and MC = 5
Value of tan M = 4/3 which is greater than 1.
Using Pythagoras theorem,
MC²=MN²+NC²
5²=3²+4²
25=9+16
25=25
(ii) True
ΔMNC in which ∠N = 90º,
MC=12k and MB=5k, where k is a positive real number.
By Pythagoras theorem,
MC²=MN²+NC²
(12k)²=(5k)²+NC²
NC²+25k²=144k²
NC²=119k²
(iii) False
Abbreviation used for cosecant of angle M is cosec M. cos M is the abbreviation used for cosine of angle M.
(iv) False
cot M is not the product of cot and M. It is the cotangent of ∠M.
(v) False
sin θ = Opposite/Hypotenuse
∴ sin θ will always less than 1 and it can never be 4/3 for any value of θ.
EXERCISE 8.2
Q. Evaluate the following :
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan² 45° + cos² 30° – sin² 60°
(iii) cos 45°/sec 30°+ cosec 30°
(iv) sin 30° + tan 45° – cosec 60°/sec 30° + cos 60° + cot 45°
(v) 5 cos² 60° + 4 sec² 30°- tan² 45°/sin² 30°+ cos² 30°
Sol. (i) sin 30° = ½
cos 30° = √3/2
sin 60° = 3/2
cos 60°= 1/2
sin 60° cos 30° + sin 30° cos 60° = √3/2 ×√3/2 + (1/2) ×(1/2 ) = 3/4+1/4 = 4/4 =1
(ii) sin 60° = √3/2
cos 30° = √3/2
tan 45° = 1
2 tan² 45° + cos² 30° – sin² 60 = 2(1)²+ (√3/2)² -(√3/2)²
2 tan² 45° + cos² 30° – sin² 60 = 2 + 0
2 tan² 45° + cos² 30° – sin² 60 = 2
(iii) cos 45° = 1/√2
sec 30° = 2/√3
cosec 30° = 2
cos 45°/sec 30°+ cosec 30°=1/√2/2/√3+2=1/√2/2+2√3/√3
=1/√2×√3/2+2√3
=1/√2×√3/2(1+√3)=√3/2√2(1+√3)=√3/2√2(√3+1)
= √3/2√2(√3+1)×√3-1/√3-1=3-√3/2√2 (3-1)=3-√3/2√2(2)
3-√3/2√2(2)×√2/√2=3√2-√3√2/8=3√2-√6/8
Therefore, cos 45°/(sec 30°+cosec 30°) = (3√2 – √6)/8
(iv) sin 30° = ½
tan 45° = 1
cosec 60° = 2/√3
sec 30° = 2/√3
cos 60° = ½
cot 45° = 1
sin 30°+tan 45°-cosec 60°/sec 30°+cos 60°+ cot 45°=½+1-2/√3/2/√3+½+1=√3+2 √3-4/2√3/4+√3+2√3/2√3
√3+2 √3-4/4+√3+2√3=3√3-4/3√3+4
3√3-4/3√3+4×3√3-4/3√3-4
27-12√3-12√3+16/27-12√3+12√3+16=27-24√3+16/11=43-24√3/11
sin 30°+tan 45°-cosec 60°/sec 30°+cos 60°+ cot 45°=43-24√3/11
(v) cos 60° = 1/2
sec 30° = 2/√3
tan 45° = 1
sin 30° = ½
cos 30° = √3/2
(5cos²60° + 4sec²30° – tan²45°)/(sin² 30° + cos² 30°)
= 5(1/2)²+4(2/√3)² -1² /(1/2)²+(√3/2)²
= (5/4+16/3-1)/(1/4+3/4)
= (15+64-12)/12/(4/4)
= 67/12
Q. Choose the correct option and justify your choice :
(i) 2 tan 30°/1+tan² 30° = (A) sin 60° (B) cos 60° (C) tan 60° (D) sin 30°
(ii) 1-tan² 45°/1+tan² 45° =
(A) tan 90° (B) 1 (C) sin 45° (D) 0
(iii) sin 2A = 2 sin A is true when A =
(A) 0° (B) 30° (C) 45° (D) 60°
(iv) 2 tan30°/1-tan² 30° =
cos 60° (B) sin 60° (C) tan 60° (D) sin 30°
Sol. (i) (A) is correct.
tan 30° = 1/√3
2 tan 30°/1+tan² 30° = 2(1/√3)/1+(1/√3)²
= (2/√3)/(1+1/3) = (2/√3)/(4/3)
= 6/4√3 = √3/2 = sin 60°
(ii) (D) is correct.
tan 45° = 1
1-tan² 45°/1+tan² 45° = (1-1²)/(1+1²)
= 0/2 = 0
(iii) (A) is correct.
sin 2A = 2 sin A is true when A = 0°
As sin 2A = sin 0° = 0
2 sin A = 2 sin 0° = 2 × 0 = 0
or, Apply the sin 2A formula, to find the degree value
sin 2A = 2sin A cos A
⇒2sin A cos A = 2 sin A
⇒ 2cos A = 2 ⇒ cos A = 1
When 0 degree is applied to cos value, i.e., cos 0 =1
Therefore, ⇒ A = 0°
(iv) (C) is correct.
tan 30° = 1/√3
2 tan 30°/1-tan² 30° = 2(1/√3)/1-(1/√3)²
= (2/√3)/(1-1/3) = (2/√3)/(2/3) = √3 = tan 60°
Q. If tan (A + B) = √3 and tan (A – B) = 1/√3 ,0° < A + B ≤ 90°; A > B, find A and B.
Sol. tan (A + B) = √3
Since √3 = tan 60°
⇒ tan (A + B) = tan 60°
(A + B) = 60° … (i)
tan (A – B) = 1/√3
Since 1/√3 = tan 30°
⇒ tan (A – B) = tan 30°
(A – B) = 30° … equation (ii)
A + B + A – B = 60° + 30°
2A = 90°
A= 45°
45° + B = 60°
B = 60° – 45°
B = 15°
Therefore A = 45° and B = 15°
Q. State whether the following are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin θ increases as θ increases.
(iii) The value of cos θ increases as θ increases.
(iv) sin θ = cos θ for all values of θ.
(v) cot A is not defined for A = 0°.
Sol. (i) False.
Let us take A = 30° and B = 60°, then
sin (A + B) = sin (30° + 60°) = sin 90° = 1,
sin A + sin B = sin 30° + sin 60°
= 1/2 + √3/2 = 1+√3/2
(ii) True
sin 0° = 0
sin 30° = 1/2
sin 45° = 1/√2
sin 60° = √3/2
sin 90° = 1
(iii) False.
cos 0° = 1
cos 30° = √3/2
cos 45° = 1/√2
cos 60° = ½
cos 90° = 0
(iv) False
sin θ = cos θ, when a right triangle has 2 angles of (π/4).
(v) True.
cot A = cos A/sin A
cot 0° = cos 0°/sin 0° = 1/0 = undefined.
EXERCISE 8.3
Q. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Sol. cosec² A– cot² A = 1
cosec² A = 1 + cot² A
1/sin² A = 1 + cot² A
sin² A = 1/(1+cot² A)
sin A = ±1/(√(1+cot² A)
sin² A = 1/ (1+cot² A)
1 – cos² A = 1/ (1+cot² A)
cos² A = 1 – 1/(1+cot² A)
⇒cos² A = (1-1+cot² A)/(1+cot² A)
⇒ 1/sec² A = cot² A/(1+cot² A)
⇒ sec A = ±√ (1+cot² A)/cotA
tan A = sin A/cos A and cot A = cos A/sin A
Since cot function is the inverse of tan function, it is rewritten as tan A = 1/cot A.
Q. Write all the other trigonometric ratios of ∠A in terms of sec A.
Sol. Cos A function in terms of sec A
sec A = 1/cos A
⇒ cos A = 1/sec A
cos² A + sin² A = 1
sin² A = 1 – cos² A
sin² A = 1 – (1/sec² A)
sin² A = (sec² A-1)/sec² A
sin A = ± √(sec² A-1)/sec A
sin A = 1/cosec A
⇒cosec A = 1/sin A
cosec A = ± sec A/√(sec2A-1)
sec² A – tan² A = 1
⇒ tan² A = sec² A – 1
tan A = √(sec² A – 1)
tan A = 1/cot A
⇒ cot A = 1/tan A
cot A = ±1/√(sec² A – 1)
Q. Choose the correct option. Justify your choice.
(i) 9 sec² A – 9 tan² A = (A) 1 (B) 9 (C) 8 (D) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)= (A) 0 (B) 1 (C) 2 (D) – 1
(iii) (sec A + tan A) (1 – sin A) = (A) sec A (B) sin A (C) cosec A (D) cos A
(iv) 1+tan² A/1+cot² A = (A) sec² A (B) -1 (C) cot² A (D) tan² A
Sol. (i) (B) is correct.
9 sec² A – 9 tan² A
= 9 (sec² A – tan² A)
= 9×1 = 9 (∵ sec2 A – tan2 A = 1)
Therefore, 9 sec² A – 9 tan² A = 9
(ii) (C) is correct
(1 + tan θ + sec θ) (1 + cot θ – cosec θ)
sec θ = 1/ cos θ
cot θ = cos θ/sin θ
cosec θ = 1/sin θ
= (1 + sin θ/cos θ + 1/ cos θ) (1 + cos θ/sin θ – 1/sin θ)
= (cos θ +sin θ+1)/cos θ × (sin θ+cos θ-1)/sin θ
= (cos θ+sin θ)² -1² /(cos θ sin θ)
= (cos² θ + sin² θ + 2cos θ sin θ -1)/(cos θ sin θ)
= (1+ 2cos θ sin θ -1)/(cos θ sin θ) (Since cos² θ + sin² θ = 1)
= (2cos θ sin θ)/(cos θ sin θ) = 2
Therefore, (1 + tan θ + sec θ) (1 + cot θ – cosec θ) =2
(iii) (D) is correct.
Sec A= 1/cos A
Tan A = sin A / cos A
(secA + tanA) (1 – sinA)
= (1/cos A + sin A/cos A) (1 – sinA)
= (1+sin A/cos A) (1 – sinA)
= (1 – sin² A)/cos A
= cos² A/cos A = cos A
Therefore, (secA + tanA) (1 – sinA) = cos A
(iv) (D) is correct.
tan² A =1/cot² A
1+tan² A/1+cot² A
= (1+1/cot² A)/1+cot² A
= (cot² A+1/cot² A)×(1/1+cot² A)
= 1/cot² A = tan² A
So, 1+tan² A/1+cot² A = tan² A
Q. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
(i) (cosec θ – cot θ)²= (1-cos θ)/(1+cos θ)
(ii) cos A/(1+sin A) + (1+sin A)/cos A = 2 sec A
(iii) tan θ/(1-cot θ) + cot θ/(1-tan θ) = 1 + sec θ cosec θ
[Hint : Write the expression in terms of sin θ and cos θ]
(iv) (1 + sec A)/sec A = sin² A/(1-cos A)
[Hint : Simplify LHS and RHS separately]
(v) ( cos A–sin A+1)/( cos A +sin A–1) = cosec A + cot A, using the identity cosec² A = 1+cot² A.
(vi) √1+ sin A/1-sin A=sec A+ tan A
(vii) (sin θ – 2sin³θ)/(2cos³θ-cos θ) = tan θ
(viii) (sin A + cosec A)²+ (cos A + sec A)² = 7+tan² A+cot² A
(ix) (cosec A – sin A)(sec A – cos A) = 1/(tan A+cotA)
[Hint : Simplify LHS and RHS separately]
(x) (1+tan² A/1+cot² A) = (1-tan A/1-cot A)² =tan² A
Sol. (i) L.H.S. = (cosec θ – cot θ)²
Since (a-b)² = a² + b² – 2ab
Here a = cosec θ and b = cot θ
= (cosec²θ + cot²θ – 2cosec θ cot θ)
= (1/sin²θ + cos²θ/sin²θ – 2cos θ/sin²θ)
= (1 + cos²θ – 2cos θ)/(1 – cos²θ)
= (1-cos θ)² /(1 – cosθ)(1+cos θ)
= (1-cos θ)/(1+cos θ) = R.H.S.
Therefore, (cosec θ – cot θ)²= (1-cos θ)/(1+cos θ)
(ii) (cos A/(1+sin A)) + ((1+sin A)/cos A) = 2 sec A
L.H.S. = (cos A/(1+sin A)) + ((1+sin A)/cos A)
= [cos²A + (1+sin A)² ]/(1+sin A)cos A
= (cos²A + sin²A + 1 + 2sin A)/(1+sin A) cos A
= (1 + 1 + 2sin A)/(1+sin A) cos A
= (2+ 2sin A)/(1+sin A)cos A
= 2(1+sin A)/(1+sin A)cos A
= 2/cos A = 2 sec A = R.H.S.
L.H.S. = R.H.S.
(cos A/(1+sin A)) + ((1+sin A)/cos A) = 2 sec A
(iii) tan θ/(1-cot θ) + cot θ/(1-tan θ) = 1 + sec θ cosec θ
L.H.S. = tan θ/(1-cot θ) + cot θ/(1-tan θ)
tan θ =sin θ/cos θ
cot θ = cos θ/sin θ
= [(sin θ/cos θ)/1-(cos θ/sin θ)] + [(cos θ/sin θ)/1-(sin θ/cos θ)]
= [(sin θ/cos θ)/(sin θ-cos θ)/sin θ] + [(cos θ/sin θ)/(cos θ-sin θ)/cos θ]
= sin²θ/[cos θ(sin θ-cos θ)] + cos²θ/[sin θ(cos θ-sin θ)]
= sin²θ/[cos θ(sin θ-cos θ)] – cos²θ/[sin θ(sin θ-cos θ)]
= 1/(sin θ-cos θ) [(sin²θ/cos θ) – (cos²θ/sin θ)]
= 1/(sin θ-cos θ) × [(sin³θ – cos³θ)/sin θ cos θ]
= [(sin θ-cos θ)(sin²θ+cos²θ+sin θ cos θ)]/[(sin θ-cos θ)sin θ cos θ]
= (1 + sin θ cos θ)/sin θ cos θ
= 1/sin θ cos θ + 1
= 1 + sec θ cosec θ = R.H.S.
Therefore, L.H.S. = R.H.S.
(iv) (1 + sec A)/sec A = sin²A/(1-cos A)
L.H.S. = (1 + sec A)/sec A
= (1 + 1/cos A)/1/cos A
= (cos A + 1)/cos A/1/cos A
Therefore, (1 + sec A)/sec A = cos A + 1
R.H.S. = sin²A/(1-cos A)
sin²A = (1 – cos²A),
= (1 – cos²A)/(1-cos A)
= (1-cos A)(1+cos A)/(1-cos A)
Therefore, sin²A/(1-cos A)= cos A + 1
L.H.S. = R.H.S.
(v) (cos A–sin A+1)/(cos A+sin A–1) = cosec A + cot A, using the identity cosec²A = 1+cot²A
L.H.S. = (cos A–sin A+1)/(cos A+sin A–1)
= (cos A–sin A+1)/sin A/(cos A+sin A–1)/sin A
= (cot A – 1 + cosec A)/(cot A+ 1 – cosec A)
= (cot A – cosec²A + cot²A + cosec A)/(cot A+ 1 – cosec A) (using cosec²A – cot²A = 1
= [(cot A + cosec A) – (cosec²A – cot²A)]/(cot A+ 1 – cosec A)
= [(cot A + cosec A) – (cosec A + cot A)(cosec A – cot A)]/(1 – cosec A + cot A)
= (cot A + cosec A)(1 – cosec A + cot A)/(1 – cosec A + cot A)
= cot A + cosec A = R.H.S
Therefore, (cos A–sin A+1)/(cos A+sin A–1) = cosec A + cot A
(vi) √1+ sin A/1-sin A=sec A+ tan A
LHS=√1+ sin A/1-sin A
= √1/cos A+ sin A/cos A/1/cos A-sin A/cos A
1/cos A = sec A and sin A/ cos A = tan A
= √(sec A+ tan A)/(sec A-tan A)
=√sec A+tan A/Sec A-tan A×√sec A+tan A/Sec +tan A
(sec A+ tan A)²/sec² A-tan² A
= (sec A + tan A)/1
= sec A + tan A = R.H.S
(vii) (sin θ – 2sin³θ)/(2cos³θ-cos θ) = tan θ
L.H.S. =(sin θ – 2sin³θ)/(2cos³θ-cos θ)
= [sin θ(1 – 2sin²θ)]/[cos θ(2cos²θ- 1)]
sin²θ = 1-cos²θ
= sin θ[1 – 2(1-cos²θ)]/[cos θ(2cos²θ -1)]
= [sin θ(2cos²θ -1)]/[cos θ(2cos²θ -1)]
= tan θ = R.H.S.
(viii) (sin A + cosec A)²+ (cos A + sec A)² = 7+tan²A+cot²A
L.H.S. = (sin A + cosec A)²+ (cos A + sec A)²
(a+b)² =a²+ b² +2ab
= (sin²A + cosec²A + 2 sin A cosec A) + (cos²A + sec²A + 2 cos A sec A)
= (sin²A + cos²A) + 2 sin A(1/sin A) + 2 cos A(1/cos A) + 1 + tan²A + 1 + cot²A
= 1 + 2 + 2 + 2 + tan²A + cot²A
= 7+tan²A+cot²A = R.H.S.
Therefore, (sin A + cosec A)²+ (cos A + sec A)² = 7+tan²A+cot²A
(ix) (cosec A – sin A)(sec A – cos A) = 1/(tan A+cotA)
L.H.S. = (cosec A – sin A)(sec A – cos A)
= (1/sin A – sin A)(1/cos A – cos A)
= [(1-sin²A)/sin A][(1-cos²A)/cos A]
= (cos²A/sin A)×(sin²A/cos A)
= cos A sin A
R.H.S. = 1/(tan A+cotA)
= 1/(sin A/cos A +cos A/sin A)
= 1/[(sin²A+cos²A)/sin A cos A]
= cos A sin A
L.H.S. = R.H.S.
(cosec A – sin A)(sec A – cos A) = 1/(tan A+cotA)
(x) (1+tan²A/1+cot²A) = (1-tan A/1-cot A)² =tan²A
L.H.S. = (1+tan²A/1+cot²A)
= (1+tan²A/1+1/tan²A)
= 1+tan²A/[(1+tan²A)/tan²A]
= tan²A
(1+tan²A/1+cot²A) = tan²A
Similarly,
(1-tan A/1-cot A)² =tan²A
To download these solutions in pdf, refer to the below link:
| Download NCERT Class 10 Maths Chapter 8 Introduction to Trigonometry Solutions PDF |
CBSE Video Courses for Class 10 Students
Class 10 students can study effectively for the exams with the help of video courses prepared by the subject matter experts. These video courses will explain the concepts in a simple and interactive manner which will help learners to understand clearly.
Also, check
CBSE Class 10 Maths Syllabus 2024-2025, Download PDF
NCERT Book for Class 10 Maths (Revised)
Comments
All Comments (0)
Join the conversation