CBSE Class 12 Maths Chapter 13 Probability Revision Notes Download PDF

CBSE Class 12 Mathematics Chapter 13 Probability Revision Notes: The 2024 board exams are here, and it is time to lay down the books and start revising the concepts. Mathematics is a subject that requires a lot of practice and thorough revision to master. In these final days before the examination, students should be wise to review what they know rather than pick new topics to learn.

The CBSE Class 12 board exams are set to start from February 15, 2024, and the mathematics paper will be held on March 9. The thirteenth chapter in the Class 12 math books is Probability. It’s one of the most important chapters in the 12th maths syllabus and holds a lot of importance in the final exam as well.

You can check out the CBSE Class 12 Chapter 13 Probability revision notes here, along with additional study resources like mind maps and multiple-choice questions.

CBSE Class 12 Maths Chapter 13 Probability Revision Notes

Basic Definitions and Summary:

1. Conditional Probability: The probability of an event E, given that the event F has already occurred is called conditional probability. It’s denoted by

P(E|F) = P(E ∩ F)/P(F) where P(F) ≠ 0

Properties of Conditional Probability:

There are three main properties of conditional probability:

If E and F be events of a sample space S of an experiment

1. i) P(S|F) = P(F|F)=1
2. ii) For any two events A and B of sample space S if F is another event such that P(F) = 0, P ((A U B) |F) =P (A|F)+P (B|F)-P ((A ∩ B)|F)

iii) P(E’|F) = 1 -P(E|F)

2. Multiplication Theorem on Probability:If E and F are independent, then P (E ∩ F) = P (E) P (F)

P (E|F) = P (E), P (F) ≠ 0

P (F|E) = P (F), P(E) ≠ 0

*Multiplication rule of probability for more than two events

If E, F and G are three events of sample space, we have 

P(E ∩ F ∩ G) = P(E) P(F|E) P(G|(E ∩ F)) = P(E) P(F|E) P(G|EF)

Similarly, the multiplication rule of probability can be extended for four or more events

If E and F are two events such that the probability of occurrence of one of them is not affected by occurrence of the other. They are called independent events.

Alternate Definition: Let E and F be two events associated with the same random experiment, then E and F are said to be independent if

P(E ∩ F) = P(E) . P (F)

3. Theorem of Total Probability: Let {E₁, E₂, ...,E_n) be a partition of a sample space and suppose that each of E₁, E₂, ..., En has a nonzero probability. Let A be any event associated with S, then P(A) = P(E₁) P (A|E₁) + P (E₂) P (A|E₂) + ... + P (E_n) P(A|E_n)
4. Bayes' Theorem:If E₁, E₂, ...,E_n are events which constitute a partition of sample space S, ie. E₁, E₂, ..., Enare pairwise disjoint and E₁ U E₂U…U E_n= S and A be any event with nonzero probability, then

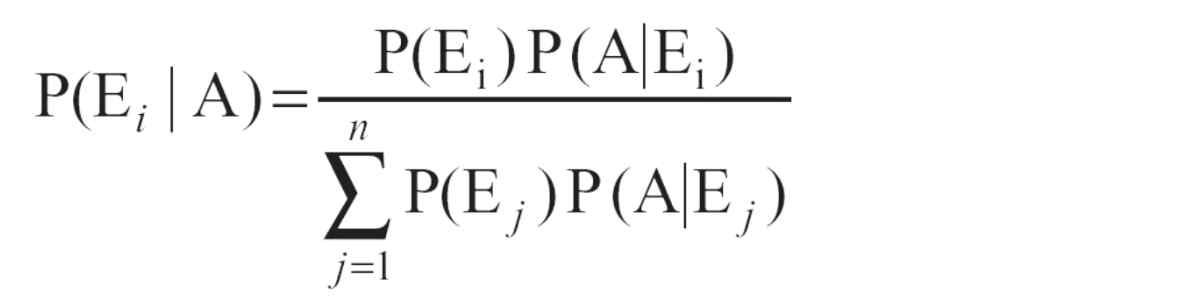
View and download the full PDF for CBSE Class 12 Mathematics Chapter 13 Probability Revision notes below.

Recommended: