NCERT Solutions for Class 10 Maths Chapter 10: NCERT solutions are a must have resource for students appearing for the board exams. The questions in the board examination are similar to the questions included in these solutions. Students can find the NCERT solutions for all subjects at Jagran Josh. These NCERT Solutions are prepared by the subject matter experts. This article consists of the detailed answers for NCERT Class 10 Maths Chapter 10 Circles.
These solutions will help students to understand the concepts and topics. Students will get an idea of how to solve questions in the examination. CBSE Class 10 Maths Chapter 10 Circles includes topics such as tangent to a circle, number of tangents from a point on a circle and more.
Students should study from NCERT Books as they help gain an understanding of concepts and strengthen their basics. They are published in accordance with the latest CBSE curriculum. These books are recommended due to their explanation of even difficult topics in simple and clear language. Questions given in the NCERT books are always considered very important as not only do they help you to analyse your understanding of the concepts involved in a chapter but also in preparing for the examinations. Students should read the chapters carefully along with attempting the questions given.
Download the NCERT Solutions for Class 10 Maths Chapter 10 from the direct link given in this article.
NCERT Class 10 Maths Chapter 10 Circles Solutions
Given below are the questions and answers of NCERT Class 10 Chapter 10 Circles.
EXERCISE 10.1
Q. How many tangents can a circle have?
Sol. A circle can have infinite tangents.
Q. Fill in the blanks :
(i) A tangent to a circle intersects it in _ point (s).
(ii) A line intersecting a circle in two points is called a_ .
(iii) A circle can have _ parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called_ .
Sol. One
Secant
Two
Point of contact
Q. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm.
Length PQ is :
(A) 12 cm
(B) 13 cm
(C) 8.5 cm
(D) √119 cm
Sol. We know that the line drawn from the centre of the circle to the tangent is perpendicular to the tangent.
And so, ∴ OP ⊥ PQ
By applying Pythagoras theorem in ΔOPQ,

∴OP²+PQ²=OQ²
5²+PQ²=12²
PQ²=144-25
PQ=√119 cm
Hence, the correct answer is (D).
Q. Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Sol. 
AB CD
Line AB is intersecting the circle at exactly two points, P and Q.
Therefore, line AB is the secant of this circle.
Since line CD is intersecting the circle at exactly one point, R, line CD is the tangent to the circle.
EXERCISE 10.2
Q. From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
Sol. 
Let O be the centre of the circle.
Given that,
OQ = 25cm and PQ = 24 cm
OP ⊥PQ (radius is perpendicular to the tangent at the point of contact)
Applying Pythagoras theorem in ΔOPQ,
OP²+PQ²=OQ²
OP²+24²=25²
OP²=625-576
OP²=49
OP=7
Therefore, the radius of the circle is 7 cm.
Hence, alternative (A) is correct
Q. In figure, if TP and TQ are the two tangents to a circle with centre O so that POQ = 110°, then PTQ is equal to
(A) 60°
(B) 70°
(C) 80°
(D) 90°
Sol. 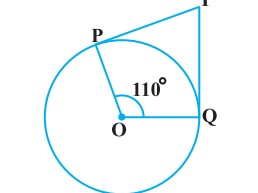
It is given that TP and TQ are tangents.
Therefore, radius drawn to these tangents will be perpendicular to the tangents.
Thus, OP ⊥TP and OQ ⊥TQ
∠OPT = 90º
∠OQT = 90º
In quadrilateral POQT,
Sum of all interior angles = 360º
∠OPT + ∠POQ +∠OQT + ∠PTQ = 360º
⇒90+ 110º + 90+∠PTQ = 360º
⇒∠PTQ = 70º
Hence, alternative (B) is correct.
Q. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠ POA is equal to
(A) 50°
(B) 60°
(C) 70°
(D) 80°
Sol. It is given that PA and PB are tangents.
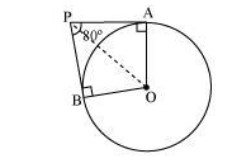
Therefore, the radius drawn to these tangents will be perpendicular to the tangents.
Thus, OA ⊥PA and OB ⊥PB
∠OBP = 90º
∠OAP = 90º
In AOBP,
Sum of all interior angles = 360º
∠OAP + ∠APB +∠PBO + ∠BOA = 360º
90º+ 80º+90º +∠BOA = 360º
∠BOA = 100º
In ΔOPB and ΔOPA,
AP = BP (Tangents from a point)
OA = OB (Radii of the circle)
OP = OP (Common side)
Therefore, ΔOPB ≅ΔOPA (SSS congruence criterion)
A ↔ B, P ↔ P, O ↔ O
And thus, ∠POB = ∠POA
∠POA=1/2∠AOB=100º/2=50º
Hence, alternative (A) is correct.
Q. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Sol. 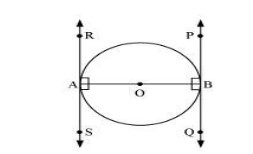
Let AB be a diameter of the circle. Two tangents PQ and RS are drawn at points A and B respectively.
Thus, OA ⊥RS and OB ⊥PQ
∠OAR = 90º
∠OAS = 90º
∠OBP = 90º
∠OBQ = 90º
It can be observed that
∠OAR = ∠OBQ (Alternate interior angles)
∠OAS = ∠OBP (Alternate interior angles)
Since alternate interior angles are equal, lines PQ and RS will be parallel.
Q. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Sol. Let us consider a circle with centre O. Let AB be a tangent which touches the circle at P.
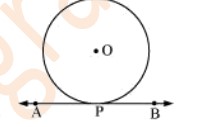
Let us assume that the perpendicular to AB at P does not pass through centre O. Let it pass through another point O’.
Join OP and O’P
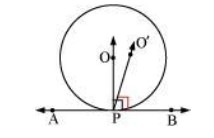
As perpendicular to AB at P passes through O’, therefore,
∠O’PB = 90° ... (1)
Line joining the centre and the point of contact to the tangent of the circle are perpendicular to each other.
∴∠OPB = 90° ... (2)
Comparing equations (1) and (2), we obtain
∠O’PB = ∠OPB ... (3)From the figure, it can be observed that,
∠O’PB < ∠OPB ... (4)
Therefore, ∠O’PB = ∠OPB is not possible. It is only possible, when the line O’P coincides with OP.
Therefore, the perpendicular to AB through P passes through centre O.
Q. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Sol. 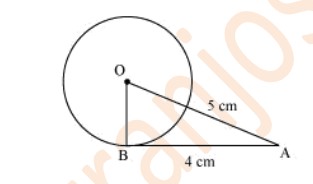
Let us consider a circle centred at point O.
AB is a tangent drawn on this circle from point A.
Given that,
OA = 5cm and AB = 4 cm
In ΔABO
OB ⊥AB (Radius ⊥tangent at the point of contact)
Applying Pythagoras theorem in ΔABO,
AB²+BO²=OA²
4²+BO²=5²
16+BO²=25
BO²=9
BO=3
Hence, the radius of the circle is 3 cm.
Q. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Sol. 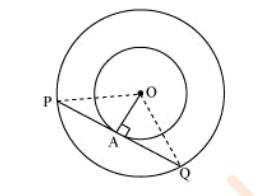
Let the two concentric circles be centred at point O. And let PQ be the chord of the larger circle which touches the smaller circle at point A. Therefore, PQ is tangent to the smaller circle.
OA ⊥PQ (As OA is the radius of the circle)
Applying Pythagoras theorem in ΔOAP, we obtain
OA²+AP²=OP²
3²+AP²=5²
9+AP²=25
AP²=16
AP=4
In ΔOPQ,
Since OA ⊥PQ,
AP = AQ (Perpendicular from the centre of the circle bisects the chord)
Thus, PQ = 2AP = 2 × 4 = 8
Therefore, the length of the chord of the larger circle is 8 cm.
Q. A quadrilateral ABCD is drawn to circumscribe a circle (see figure). Prove that AB + CD = AD + BC.
Sol. 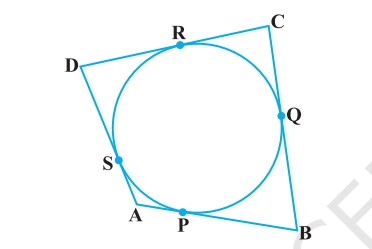
It can be observed that
DR = DS (Tangents on the circle from point D) ... (1)
CR = CQ (Tangents on the circle from point C) ... (2)
BP = BQ (Tangents on the circle from point B) ... (3)
AP = AS (Tangents on the circle from point A) ... (4)
Adding all these equations, we obtain
DR + CR + BP + AP = DS + CQ + BQ + AS
(DR + CR) + (BP + AP) = (DS + AS) + (CQ + BQ)
CD + AB = AD + BC
Q. In the figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that AOB = 90°.
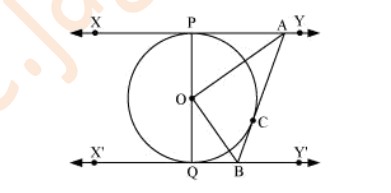
Sol. Let us join point O to C.
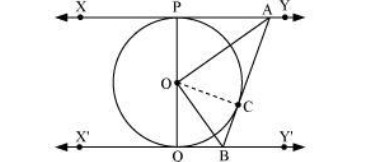
In ΔOPA and ΔOCA,
OP = OC (Radii of the same circle)
AP = AC (Tangents from point A)
AO = AO (Common side)
ΔOPA≅ΔOCA (SSS congruence criterion)
Therefore, P ↔ C, A ↔ A, O ↔ O
∠POA = ∠COA ... (i)
Similarly, ΔOQB≅ΔOCB
∠QOB = ∠COB ... (ii)
Since POQ is a diameter of the circle, it is a straight line.
Therefore, ∠POA + ∠COA + ∠COB + ∠QOB = 180º
From equations (i) and (ii), it can be observed that
2∠COA + 2 ∠COB = 180º
∠COA + ∠COB = 90º
∠AOB = 90°
Q. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Sol. 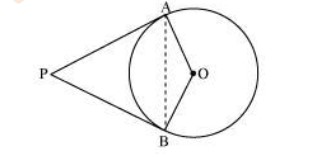
Let us consider a circle centred at point O. Let P be an external point from which two tangents PA and PB are drawn to the circle which are touching the circle at point A and B respectively and AB is the line segment, joining point of contacts A and B together such that it subtends ∠AOB at centre O of the circle.
OA (radius) ⊥PA (tangent)
Therefore, ∠OAP = 90°
Similarly, OB (radius) ⊥PB (tangent)
∠OBP = 90°
In quadrilateral OAPB,
Sum of all interior angles = 360º
∠OAP +∠APB+∠PBO +∠BOA = 360º
90º + ∠APB + 90º + ∠BOA = 360º
∠APB + ∠BOA = 180º
Hence, it can be observed that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Q. Prove that the parallelogram circumscribing a circle is a rhombus.
Sol. Since ABCD is a parallelogram,
AB = CD ...(1)
BC = AD ...(2)
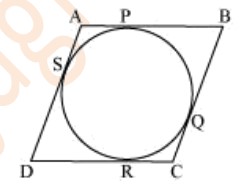
DR = DS (Tangents on the circle from point D)
CR = CQ (Tangents on the circle from point C)
BP = BQ (Tangents on the circle from point B)
AP = AS (Tangents on the circle from point A)
Adding all these equations, we obtain
DR + CR + BP + AP = DS + CQ + BQ + AS
(DR + CR) + (BP + AP) = (DS + AS) + (CQ + BQ)
CD + AB = AD + BC
On putting the values of equations (1) and (2) in this equation, we obtain
2AB = 2BC
AB = BC ...(3)
Comparing equations (1), (2), and (3), we obtain
AB = BC = CD = DA
Hence, ABCD is a rhombus.
Q. A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.

Sol. Let the given circle touch the sides AB and AC of the triangle at point E and F respectively and the length of the line segment AF be x.
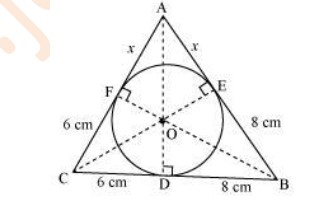
In ABC,
CF = CD = 6cm (Tangents on the circle from point C)
BE = BD = 8cm (Tangents on the circle from point B)
AE = AF =x(Tangents on the circle from point A)
AB = AE + EB =x+ 8
BC = BD + DC = 8 + 6 = 14
CA = CF + FA = 6 +x
2s =AB + BC + CA
=x+ 8 + 14 + 6 +x
=28 + 2x
s= 14 +x
Area of ABC= √s (s-a) (s-b) (s-c)
=√(14+ x) (14+x-14) (14+x-6-x) (14+ x-8-x)
= 4 √3x (14+x)
Area of ΔOBC= 1/2×OD×BC=1/2×4×14=28
Area of ΔOCA =1/2×OF×AC=1/2×4×(6+x)=12+2x
Area of ΔOAB =1/2×OE×AB=1/2×4×(8+x)=16+2x
Area of ΔABC = Area of ΔOBC + Area of ΔOCA + Area of ΔOAB
4 √3x(14+x)=28+12+2x+16+2x
4 √3x(14+x)=56+4x
√3x(14+x)=14+x
3x(14+x)=196+x²+28x
42x+3x²=196+x²+28x
2x²+14x-196=0
x²+7x-98=0
x²+14x-7x-98=0
x(x+14)-7(x+14)=0
(x+14) (x-7)=0
x=7, -14
However, x= −14 is not possible as the length of the sides will be negative.
Therefore, x= 7
Hence, AB =x+ 8 = 7 + 8 = 15 cm
CA = 6 +x= 6 + 7 = 13 cm
Q. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Sol. 
Let ABCD be a quadrilateral circumscribing a circle centred at O such that it touches the circle at point P, Q, R, S. Let us join the vertices of the quadrilateral ABCD to the centre of the circle.
Consider ΔOAP and ΔOAS,
AP = AS (Tangents from the same point)
OP = OS (Radii of the same circle)
OA = OA (Common side)
ΔOAP ≅ΔOAS (SSS congruence criterion)
Therefore, A ↔ A, P ↔ S, O ↔ O
And thus, ∠POA = ∠AOS
∠1 = ∠8
Similarly,
∠2 = ∠3
∠4 = ∠5
∠6 = ∠7
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360º
(∠1 + ∠8) + (∠2 + ∠3) + (∠4 + ∠5) + (∠6 + ∠7) = 360º
2∠1 + 2∠2 + 2∠5 + 2∠6 = 360º
2(∠1 + ∠2) + 2(∠5 + ∠6) = 360º
(∠1 + ∠2) + (∠5 + ∠6) = 180º
∠AOB + ∠COD = 180º
Similarly, we can prove that ∠BOC + ∠DOA = 180º
Hence, opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
To download these solutions in pdf, refer to the below link:
| Download NCERT Class 10 Maths Chapter 10 Circles Solutions PDF |
CBSE Video Courses for Class 10 Students
Class 10 students can study effectively for the exams with the help of video courses prepared by the subject matter experts. These video courses will explain the concepts in a simple and interactive manner which will help learners to understand clearly.
Also, check
CBSE Class 10 Maths Syllabus 2024-2025, Download PDF
NCERT Exemplar Solutions for Class 10 Maths
NCERT Book for Class 10 Maths (Revised)
CBSE Class 10 Maths Deleted Syllabus for 2025 Board Exam
Prime Numbers: Definition, Properties, Examples, List Upto 1000 and Applications
Pythagoras Theorem: Definition, Formula, Proof, Examples and Applications
Comments
All Comments (0)
Join the conversation